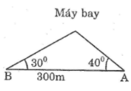
Hai người từ hai vị trí quan sát B và C nhìn thấy một chiếc máy bay trực thăng (ở vị trí A) lần lượt dưới góc 27o ( o ABC 27 ) và 25o ( o ACB 25 )so với phương nằm ngang (trên hình 1). Biết máy bay đang cách mặt đất theo phương thẳng đứng 300 m.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 12 2023
Câu 3:
Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)
=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)
=>\(CA\simeq183,85\left(m\right)\)
Câu 4:
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔABE vuông tại A có AC là đường cao
nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)
b: Ta có: ΔOAD cân tại O
mà OE là đường cao
nên OE là phân giác của góc AOD
Xét ΔOAE và ΔODE có
OA=OD
\(\widehat{AOE}=\widehat{DOE}\)
OE chung
Do đó: ΔOAE=ΔODE
=>\(\widehat{OAE}=\widehat{ODE}=90^0\)
Xét tứ giác EAOD có
\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
=>EAOD là tứ giác nội tiếp
=>E,A,O,D cùng thuộc một đường tròn
c: Xét (O) có
OD là bán kính
ED\(\perp\)DO tại D
Do đó: ED là tiếp tuyến của (O)
Xét (O) có
\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC
\(\widehat{CBD}\) là góc nội tiếp chắn cung DC
Do đó: \(\widehat{EDC}=\widehat{CBD}\)
=>\(\widehat{EDC}=\widehat{EBD}\)
Xét ΔEDC và ΔEBD có
\(\widehat{EDC}=\widehat{EBD}\)
\(\widehat{DEC}\) chung
Do đó: ΔEDC đồng dạng với ΔEBD
=>\(\widehat{ECD}=\widehat{EDB}\)
CM
20 tháng 8 2018
Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
Xét tam giác ADC vuông tại C có:
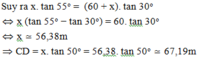
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
CM
28 tháng 1 2019
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
CM
2 tháng 9 2018
Gọi C là vị trí của máy bay.
Kẻ CH ⊥ AB
Trong tam giác vuông ACH, ta có:
AH = CH.cotgA (1)
Trong tam giác vuông BCH, ta có:
BH = CH.cotgB (2)
Từ (1) và (2) suy ra: (AH + BH) = CH.cotgA + CH.cotgB
Suy ra: CH =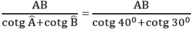 
≈ 102,606 (cm)
2 tháng 12 2023
Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
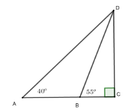
Ta có hình vẽ sau:
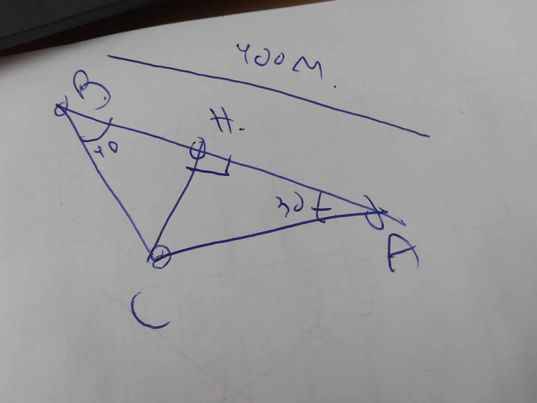
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)
1 tháng 8 2023
Gọi giao điểm của đường nhìn thấy máy bay tại A và B là C.
Vẽ CH vuông góc AB
=>CH là độ cao của máy bay
góc ACB=180-40-32=108 độ
Xét ΔACB có
AB/sin C=AC/sinB=BC/sin A
=>400/sin108=AC/sin32=BC/sin40
=>\(AC\simeq222,9\left(m\right);BC\simeq270,3\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinC=\dfrac{1}{2}\cdot222.9\cdot270.3\cdot sin108\simeq28650,52\left(m^2\right)\)
Độ cao là:"
28650,52*2/400\(\simeq143\left(m\right)\)
PT
26 tháng 7 2017
Gọi C là vị trí của máy bay.
Kẻ CH⊥ABCH⊥AB
Trong tam giác vuông ACH, ta có:
AH=CH.cotgˆA(1)AH=CH.cotgA^(1)
Trong tam giác vuông BCH, ta có:
BH=CH.cotgˆB(2)BH=CH.cotgB^(2)
Từ (1) và (2) suy ra:
(AH+BH)=CH.cotgˆA+CH.cotgˆB(AH+BH)=CH.cotgA^+CH.cotgB^
Suy ra:
CH=ABcotgˆA+cotgˆB=ABcotg40∘+cotg30∘≈102,606(cm)
3 tháng 8 2021
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m