Tam giác ABC vuông tại A, có AC = (1/2).BC. Tính sinB, cosB, tgB, cotgB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
1
AH
Akai Haruma
Giáo viên
27 tháng 10 2018
Lời giải:
Đặt \(AC=\frac{BC}{2}=a\) \(\Rightarrow BC=2a\)
Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=\sqrt{(2a)^2-a^2}=\sqrt{3}a\)
Vậy:
\(\sin B=\frac{AC}{BC}=\frac{a}{2a}=\frac{1}{2}\)
\(\cos B=\frac{AB}{BC}=\frac{\sqrt{3}a}{2a}=\frac{\sqrt{3}}{2}\)
\(\tan B=\frac{AC}{AB}=\frac{a}{\sqrt{3}a}=\frac{1}{\sqrt{3}}\)
\(\cot B=\frac{AB}{AC}=\frac{\sqrt{3}a}{a}=\sqrt{3}\)
29 tháng 10 2018
mình gửi từ tháng 8 năm 2017 mà bây giờ tháng 10 năm 2018 rồi thì bạn trả lời làm gì nữa ?
NM
23
12 tháng 6 2016
Vì sinB = \(\frac{3}{5}\) , ta có : sin2B + cos2B = 1
nên cos2B = 1 - sin2B = 1 - ( \(\frac{3}{5}\) )2 = 1 - \(\frac{9}{25}\) = \(\frac{16}{25}\)
Vậy cosB = \(\frac{4}{5}\) ( vì cosB > 0 )
Suy ra : tgB = sinB : cosB = \(\frac{3}{5}\) : \(\frac{4}{5}\) = \(\frac{3}{4}\)
cotgB = cosB : sinB = \(\frac{4}{5}\) : \(\frac{3}{5}\) = \(\frac{4}{3}\)
PN
17 tháng 7 2020
mình trả lời hơi muộn :(
1, Theo giả thiết ta có C = 45* nên tam giác ABC là tam giác vuông cân
Suy ra AB = AC = 2 (cm) Mà theo đánh giá của Pitago thì :BC^2 = 8 <=> BC = căn 8
Ta có hệ thức lượng sau : AB.AC=AH.BC <=> 4=căn 8 . AH<=> AH=2/căn2
Lại có hệ thức lượng sau : AC^2=CH.BC<=>4=căn 8 . CH <=> CH=2/căn2
Mặt khác : +)Cos alpha = AB/BC = 2/căn8 = 1/căn2
+)Cos beta = AC/BC = 2/căn8 = 1/căn2
+) Sin alpha = AC/BC = 2/căn8 = 1/căn2
+) Sin beta = AB/BC = 2/căn8 = 1/căn2
Vậy ...
Mấy câu còn lại để từ từ mình làm dần
CM
15 tháng 7 2017
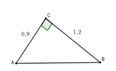
Theo định lý Py-ta-go ta có:
Xét tam giác ABC vuông tại C có:
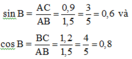
Đáp án cần chọn là: A
T
0
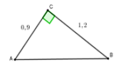
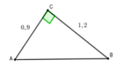
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 ⇒ A B 2 = B C 2 - A C 2