Giải giúp em bài này gấp với ạ :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)


a) \(\left\{{}\begin{matrix}2x-7>0.\\5x+1>0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x>7.\\5x>-1.\end{matrix}\right.\) \(\left\{{}\begin{matrix}x>\dfrac{7}{2}.\\x>\dfrac{-1}{5}.\end{matrix}\right.\)
\(\Rightarrow x>\dfrac{7}{2}.\) \(\Rightarrow x\in\left(\dfrac{7}{2};+\infty\right).\)
Kết luận: Tập nghiệm của hệ bất phương trình trên là \(x\in\left(\dfrac{7}{2};+\infty\right).\)
b) \(\left\{{}\begin{matrix}\left(2x+3\right)\left(x-1\right)>0.\\7x-5< 0.\end{matrix}\right.\) \(\Leftrightarrow\text{}\text{}\)\(\left\{{}\begin{matrix}\left(2x+3\right)\left(x-1\right)>0.\left(1\right)\\x< \dfrac{5}{7}.\left(2\right)\end{matrix}\right.\)
Xét (1):
\(2x+3=0.\Leftrightarrow x=\dfrac{-3}{2}.\\ x-1=0.\Leftrightarrow x=1.\)
Bảng xét dấu:
\(x\) \(-\infty\) \(\dfrac{-3}{2}\) \(1\) \(+\infty\)
\(2x+3\) - \(0\) + | +
\(x-1\) - | - \(0\) +
\(\left(2x+3\right)\left(x-1\right)\) + \(0\) - \(0\) +
Vậy \(\left(2x+3\right)\left(x-1\right)>0.\Leftrightarrow\dfrac{-3}{2}< x< 1.\)
Kết hợp với (2).
\(\Rightarrow\) \(\dfrac{-3}{2}< x< \dfrac{5}{7}.\)
\(\Rightarrow x\in\left(\dfrac{-3}{2};\dfrac{5}{7}\right).\)
Kết luận: Tập nghiệm của hệ bất phương trình trên là \(x\in\left(\dfrac{-3}{2};\dfrac{5}{7}\right).\)

Lời giải:
Để $x^4+2x^3-ax^2+5x+b$ chia $x^2+x-2$ dư $3x+4$ thì:
$x^4+2x^3-ax^2+5x+b=(x^2+x-2)Q(x)+3x+4$ với $Q(x)$ là đa thức thương.
$\Leftrightarrow x^4+2x^3-ax^2+5x+b=(x-1)(x+2)Q(x)+3x+4$
Cho $x=1$ thì:
$8-a+b=7\Leftrightarrow a-b=1(1)$
Cho $x=-2$ thì:
$-10-4a+b=-2\Leftrightarrow -4a+b=8(2)$
Từ $(1); (2)\Rightarrow a=-3; b=-4$

1/ \(B=2\pi.10^{-7}.\dfrac{NI}{r}\Rightarrow I=\dfrac{B.r}{2\pi.10^{-7}.N}=\dfrac{6,28.10^{-6}.0,05}{2\pi.10^{-7}.100}=...\left(A\right)\)
2/ \(\phi=NBS\cos\alpha=500.0,4.4.10^{-3}.\cos0^0=0,8\left(Wb\right)\)
b/ \(\xi=\dfrac{\Delta\phi}{\Delta t}=\dfrac{2.0,8-0,8}{0,02}=40\left(V\right)\)
3/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow-\dfrac{1}{20}=\dfrac{1}{20}+\dfrac{1}{d'}\Rightarrow d'=-10\left(cm\right)\)
\(\Rightarrow k=-\dfrac{d'}{d}=\dfrac{10}{20}=\dfrac{1}{2}\Rightarrow A'B'=\left|k\right|AB=\dfrac{1}{2}.AB\)
Anh ao, cung chieu, bang mot nua vat
P/s: Ban tu ve hinh

vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )




 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ






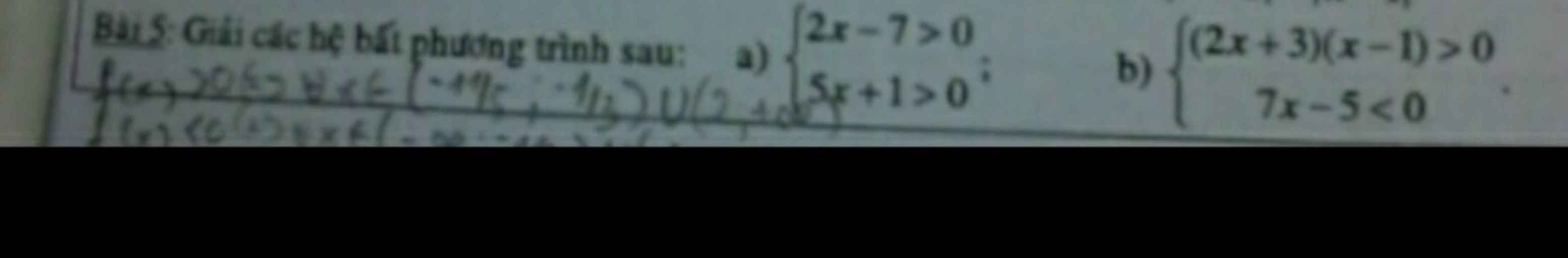
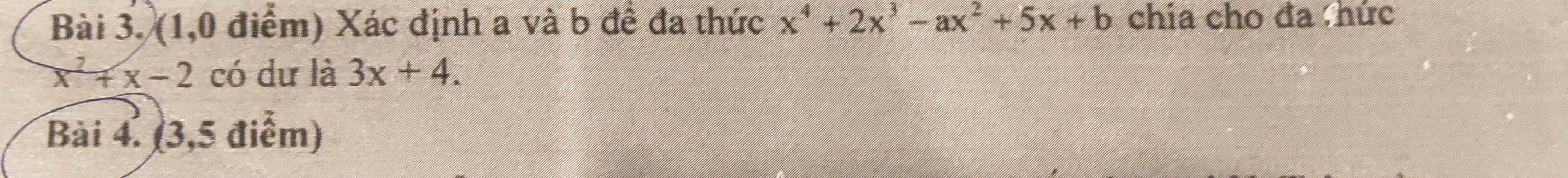 Mọi ng giúp em giải bài này với ạ, em cần gấp.
Mọi ng giúp em giải bài này với ạ, em cần gấp.

?