Em đang cần gấp mong anh chị giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) ĐKXĐ: \(x\ge0\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge4\)
4) ĐKXĐ: \(x>16\)
5) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge0\end{matrix}\right.\)
6) ĐKXĐ: \(\left[{}\begin{matrix}x\le-1\\x\ge4\end{matrix}\right.\)
7) ĐKXĐ: \(\left[{}\begin{matrix}1\le x\\x< 3\end{matrix}\right.\)
8) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x>3\end{matrix}\right.\)
9) ĐKXĐ: \(x\in R\)
10) ĐKXĐ: \(x\in R\)
11) ĐKXĐ: \(x\in R\)
12) ĐKXĐ: \(x\in R\)
13) ĐKXĐ: \(x\in R\)
14) ĐKXĐ: \(x\in R\)
15) ĐKXĐ: \(x\in R\)
16) ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
17) ĐKXĐ: \(x\ge7\)
18) ĐKXĐ: \(x\ge-5\)




Bài 6:
a. \(A=[\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{2}{\sqrt{x}(\sqrt{x}-1)}].(\sqrt{x}-1)\)
\(=\sqrt{x}+\frac{2}{\sqrt{x}}=\frac{x+2}{\sqrt{x}}\)
b. Áp dụng BĐT Cô-si cho các số dương:
$A=\sqrt{x}+\frac{2}{\sqrt{x}}\geq 2\sqrt{2}$
Vậy gtnn của $A$ là $2\sqrt{2}$. Giá trị này đạt tại $x=2$
Bài 7:
a.
\(x=\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}=1\)
Khi đó: \(B=\frac{1+3}{1+8}=\frac{4}{9}\)
b. \(A=\frac{(\sqrt{x}+1)(\sqrt{x}+3)+\sqrt{x}(2\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}-\frac{x+6\sqrt{x}+2}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{3x+3\sqrt{x}+3-(x+6\sqrt{x}+2)}{(\sqrt{x}+3)(2\sqrt{x}-1)}=\frac{2x-3\sqrt{x}+1}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{(2\sqrt{x}-1)(\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}=\frac{\sqrt{x}-1}{\sqrt{x}+3}\)
c.
\(P=AB=\frac{\sqrt{x}+3}{x+8}.\frac{\sqrt{x}-1}{\sqrt{x}+3}=\frac{\sqrt{x}-1}{x+8}\)
Áp dụng BĐT Cô-si:
$x+16\geq 8\sqrt{x}$
$\Rightarrow x+8\geq 8(\sqrt{x}-1)$
$\Rightarrow P\leq \frac{\sqrt{x}-1}{8(\sqrt{x}-1)}=\frac{1}{8}$
Vậy $P_{\max}=\frac{1}{8}$ khi $x=16$

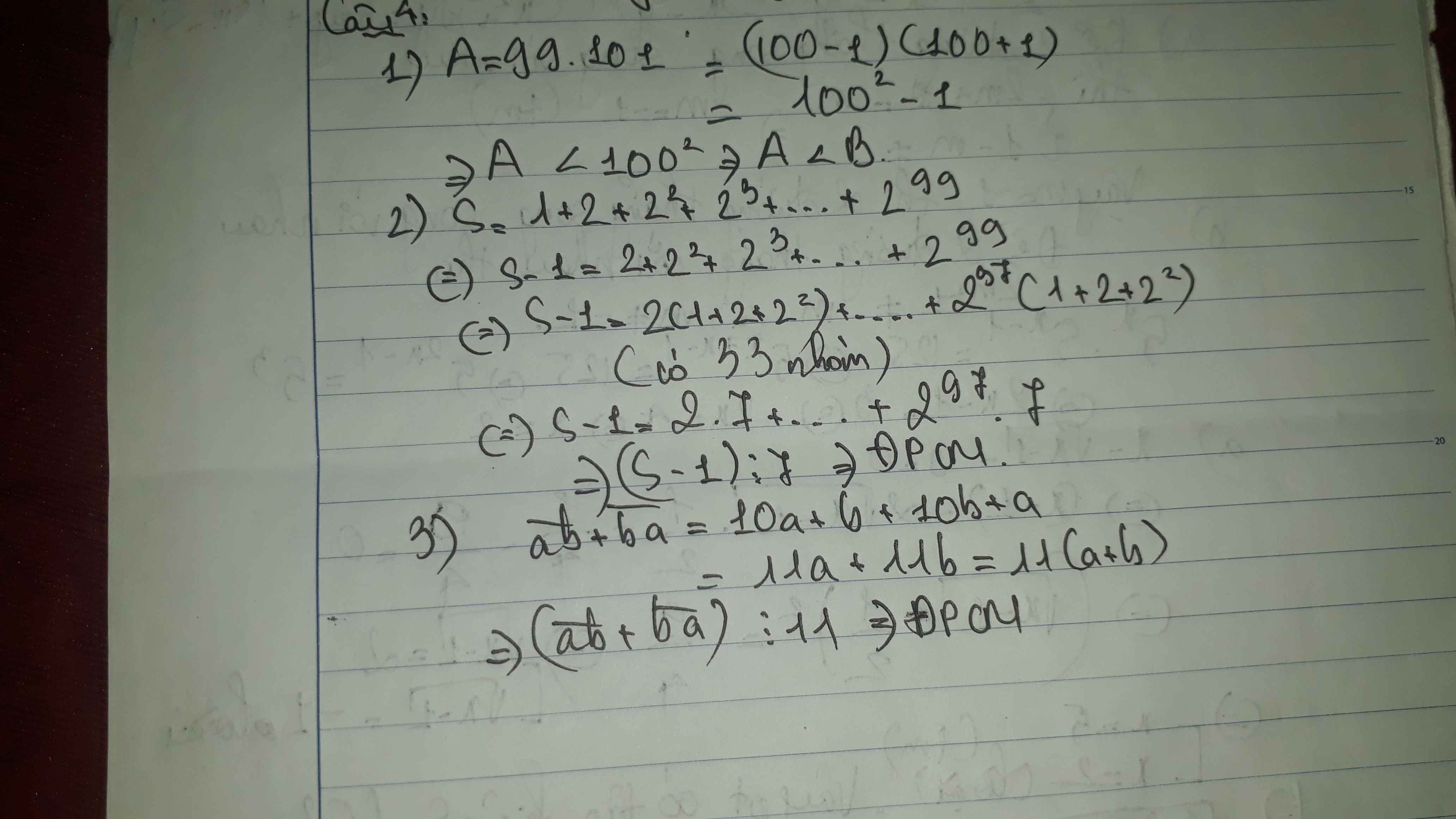






 Anh chị nào bt thì giúp em với ạ. Em đang cần gấp
Anh chị nào bt thì giúp em với ạ. Em đang cần gấp

Gọi CTHH của phân tử là: \(Na_2CO_3.nH_2O\)
Theo đề, ta có: \(\dfrac{106}{106+18n}.100\%=37,07\%\)
\(\Leftrightarrow n\approx10\)
Vậy CTHH của phân tử là: Na2CO3.10H2O
Chọn C