Cho hình chóp S.ABC có độ dài cạnh S A = B C = x , S B = A C = y , S C = A B = z thỏa mãn điều kiện x 2 + y 2 + z 2 = 9 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC
A. 3 6 8
B. 3 6 4
C. 6 4
D. 2 6 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Ghép hình chóp vào hình hộp chữ nhật có 3 kích thước là a, b, c.
Ta có a 2 + b 2 = x 2 b 2 + c 2 = y 2 ⇒ a 2 + b 2 + c 2 = x 2 + y 2 + z 2 2 c 2 + a 2 = z 2 ⇒ c 2 = y 2 + z 2 - x 2 2 a 2 = x 2 + z 2 - y 2 2 b 2 = x 2 + y 2 - z 2 2
⇒ a b c = y 2 + z 2 - x 2 x 2 + z 2 - y 2 x 2 + y 2 - z 2 8 .
Thể tích khối chóp S.ABCD là V = 1 3 a b c = 12 12 y 2 + z 2 - x 2 x 2 + z 2 - y 2 x 2 + y 2 - z 2 .
≤ 1 6 2 y 2 + z 2 - x 2 + x 2 + z 2 - y 2 + x 2 + y 2 - z 2 3 3 = 1 6 2 . 3 3 = 6 4 .
Vậy giá trị lớn nhất của V S . A B C D là 6 4 .

Đáp án C
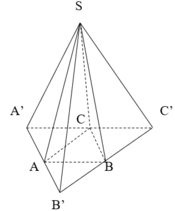
Dựng hình chóp SA’B’C’ sao cho A là trung điểm A’B’, B là trung điểm B’C’, C là trung điểm A’C’.
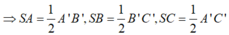
Suy ra SA’,SB’,SC’ đôi một vuông góc với nhau
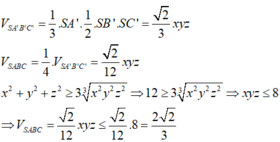

Đáp án C
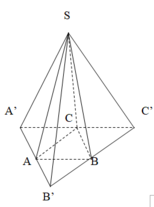
Dựng hình chóp SA’B’C’ sao cho A là trung điểm A’B’, B là trung điểm B’C’, C là trung điểm A’C’.
⇒ S A = 1 2 A ' B ' , S B = 1 2 B ' C ' , S C = 1 2 A ' C '
Suy ra SA’,SB’,SC’ đôi một vuông góc với nhau
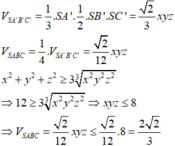

Đáp án A
Thể tích khối chóp S.ABC là:
V S . A B C = 2 12 . x 2 + y 2 − z 2 y 2 + z 2 − x 2 x 2 + z 2 − y 2
Mà: x 2 + y 2 − z 2 y 2 + z 2 − x 2 x 2 + z 2 − y 2
≤ x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + x 2 + z 2 − y 2 27
= x 2 + y 2 + z 2 3 27
Suy ra: S . A B C ≤ 2 12 . x 2 + y 2 + z 2 27
= 2 12 . 12 3 27 = 2 2 3
Vậy: V max = 2 2 3

Đáp án C
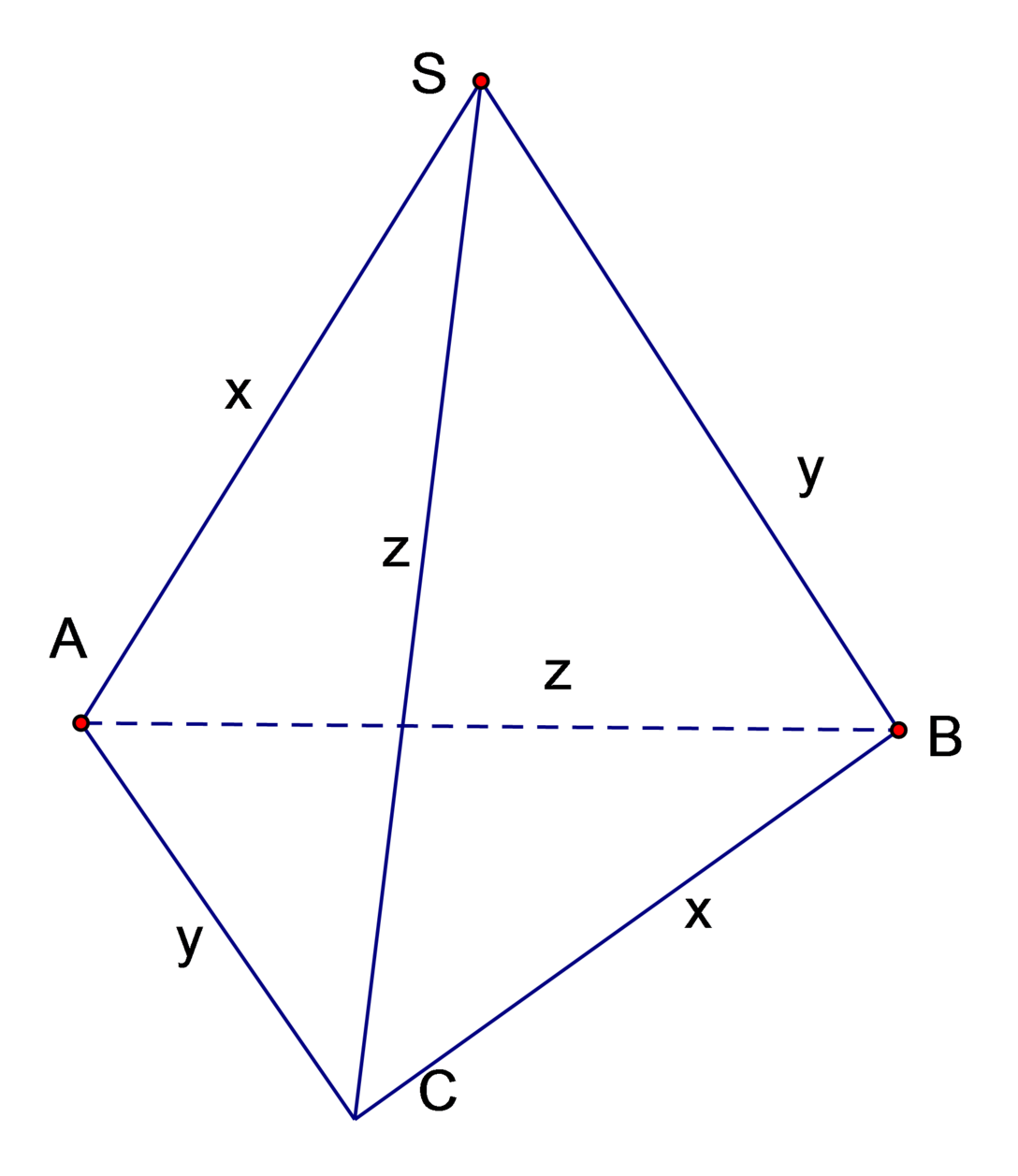
Áp dụng công thức tính thể tích tứ diện có hai cặp cạnh đối bằng nhau:
V S A B C = 1 6 2 x 2 + y 2 − z 2 y 2 + z 2 − x 2 z 2 + x 2 − y 2 ≤ 1 6 2 x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + z 2 + x 2 − y 2 3 3 = 1 6 2 x 2 + y 2 + z 2 3 3 = 1 6 2 12 3 3 = 1 6 2 .8 = 2 2 3
Như vậy V S A B C lớn nhất bằng 2 2 3 khi: x=y=z=2

a: Xét ΔEAF và ΔEBC có
góc EAF=góc EBC
góc AEF=góc BEC
=>ΔEAF đồng dạng với EBC
b: ΔEAF đồng dạng với ΔEBC
=>EF/EC=AF/BC=AE/EB
=>EF/5=2/4=1/2
=>EF+2,5cm
Đáp án là C