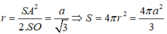Giúp nhea! Cho tứ diện SABCD có SA, SB, SC đôi một vuông góc. H là trực tâm tam giác ABC. O là đường tròn ngoại tiếp tam giác ABC
CMR:(OH2)/(SH2)+2=1/(4∗cosA∗cosB∗cosC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 1 2019
Đáp án B
Gọi M,N lần lượt là trung điểm SC, AB
Vì ΔSAB vuông góc tại S nên N là tâm đường tròn ngoại tiếp ΔSAB .
Trong mặt phẳng (MSN) dựng hình chữ nhật MSNO thì ON là trục đường tròn ngoại tiếp ΔSAB và OM là đường trung trực của đoạn SC trong mặt phẳng (OSC)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
Do \(SO\perp ABC\Rightarrow\) các tam giác SOA, SOB, SOC đều vuông tại O
Đặt \(SA=SB=SC=a\) , áp dụng Pitago:
\(OA=\sqrt{SA^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OB=\sqrt{SB^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OC=\sqrt{SC^2-SO^2}=\sqrt{a^2-SO^2}\)
\(\Rightarrow OA=OB=OC\Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác ABC
30 tháng 5 2021
SH vuông góc (ABC) => AC vuông góc SH, mà AC vuông góc BH nên AC vuông góc (SHB)
=> SB vuông góc AC, kết hợp với SB vuông góc SA => SB vuông góc SC => SA,SB,SC đôi một vuông góc
Từ đó, theo định lì Pytago và BĐT \(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}\):
\(6\left(SA^2+SB^2+SC^2\right)=3\left(AB^2+BC^2+CA^2\right)\ge3.\frac{\left(AB+BC+CA\right)^2}{3}=\left(AB+BC+CA\right)^2\)
CM
24 tháng 10 2019
Đáp án B
Từ giả thiết ta có SO là trục của đường tròn ngoại tiếp tam giác ABC và SA=SB=a. Trong mặt phẳng (SAO), trung trực của cạnh SA cắt SO tại I thì I là tâm của mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được:
