Cho hàm số Tập hợp các giá trị của x để là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(y=\dfrac{2x^2+1}{x^2}\)
\(\Rightarrow y'=\dfrac{\left(4x+1\right)x^2-2x\left(2x^2+1\right)}{x^4}\)
\(\Leftrightarrow y'=\dfrac{4x^3+x^2-4x^3-2x}{x^4}\)
\(\Leftrightarrow y'=\dfrac{x^2-2x}{x^4}=\dfrac{x\left(x-2\right)}{x^4}=\dfrac{x-2}{x^3}\)
2) \(f\left(x\right)=\sqrt[]{-5x^2+14x-9}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-10x+14}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-2\left(5x-7\right)}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}\)
Để \(f'\left(x\right)=0\)
\(f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}=0\)
\(\Leftrightarrow5x-7=0\)
\(\Leftrightarrow5x=7\)
\(\Leftrightarrow x=\dfrac{7}{5}\)
Vậy tập hợp giá trị để \(f'\left(x\right)=0\) là \(\left\{\dfrac{7}{5}\right\}\)

2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)

Đáp án D
- Phương pháp: Sử dụng công thức 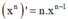 và
và 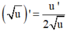 tính f'(x). Từ đó giải bất phương trình.
tính f'(x). Từ đó giải bất phương trình.
- Cách giải:
+ Ta có: 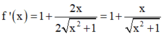
+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.
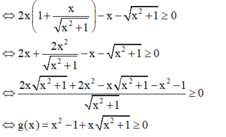
+ Thử các đáp án:
+ Với 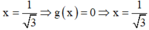 thuộc tập nghiệm của BPT.
thuộc tập nghiệm của BPT.
⇒ Loại đáp án A, B và C.

Đáp án D
- Phương pháp: Sử dụng công thức 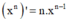 và
và 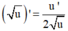 tính f'(x). Từ đó giải bất phương trình.
tính f'(x). Từ đó giải bất phương trình.
- Cách giải:
+ Ta có: 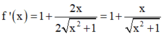
+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.
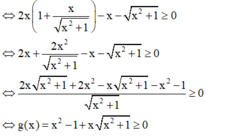
+ Thử các đáp án:
+ Với 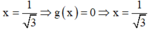 thuộc tập nghiệm của BPT.
thuộc tập nghiệm của BPT.
⇒ Loại đáp án A, B và C.


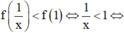


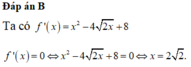
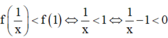
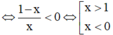
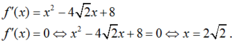


Đáp án A.
f ' x = − 10 x + 14 − 5 x 2 + 14 x − 9 với 1 < x < 9 5 . f ' x < 0 ⇔ − 10 x + 14 0 ⇔ x 14 10 = 7 5 .
Kết hợp với điều kiện thì x ∈ 7 5 ; 9 5 .