Cho hình lăng trụ đứng
A
B
C
.
A
'
B
'
C
'
có đáy là
A
B
C
là tam giác vuông
B
A
=
B
C
=
a
, cạnh bên
AA
'
=
a
2
.Gọi
M
là trung điểm của
B
C
. Tính khoảng cách giữa hai đường thẳng
A
M
,
B
'
C
'
. A.
d
A
M
,
B
'
C
=
a
7
7
B.
d
...
Đọc tiếp
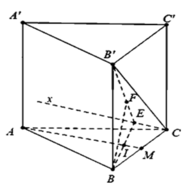
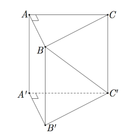
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy là A B C là tam giác vuông B A = B C = a , cạnh bên AA ' = a 2 .Gọi M là trung điểm của B C . Tính khoảng cách giữa hai đường thẳng A M , B ' C ' .
A. d A M , B ' C = a 7 7
B. d A M , B ' C = a 2 2
C. d A M , B ' C = a 3 3
D. d A M , B ' C = a 5 5
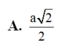
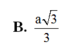
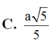
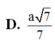
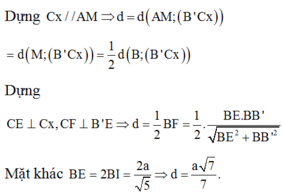
Đáp án là A
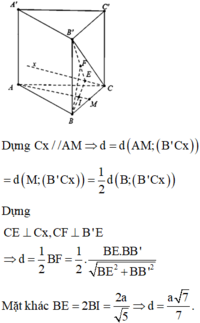
Gọi E là trung điểm của B B ' . Khi đó B ' C / / A M E ⇒ d A M ; B ' C = d B ' C ; A M E .
Mặt khác d B ; A M E = d C ; A M E . Gọi h = d B ; A M E
Vì tứ diện B A M E có B A ; B M ; B E đôi một vuông góc với nhau.
⇒ 1 h 2 = 1 B A 2 + 1 B M 2 + 1 B E 2 ⇒ 1 h 2 = 1 a 2 + 4 a 2 + 2 a 2 = 7 a 2 ⇒ h = a 7 7 ⇒ d B ' C ; A M = a 7 7 .