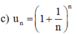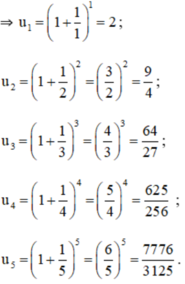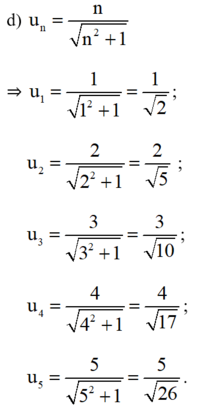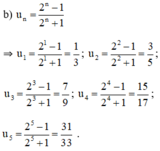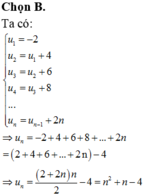Viết năm số hạng đầu của dãy số có số hạng tổng quát u n cho bởi công thức: u n = n n 2 - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
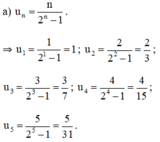
a) \({u_1} = 1\)
\( \Rightarrow {u_2} = 2.1 = 2\)
\( \Rightarrow {u_3} = 3.2 = 6\)
\( \Rightarrow {u_4} = 4.6 = 24\)
\( \Rightarrow {u_5} = 5.24 = 120\)
b)
Ta có:
\({u_2} = 2 = 2.1 \)
\({u_3} = 6= 1.2.3 \)
\({u_4} = 24 = 1.2.3.4\)
\({u_5} = 120 = 1.2.3.4.5\)
\( \Rightarrow {u_n} = 1.2.3....n = n!\).
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Năm số hạng đầu của dãy số là: 3; 9; 19; 33; 51
b) Năm số hạng đầu của dãy số là: \( - 1;\frac{1}{3}; - \frac{1}{5};\frac{1}{7}; - \frac{1}{9}\)
c) Năm số hạng đầu của dãy số là: \(2;2;\frac{8}{3};4;\frac{{32}}{5}\)
d) Năm số hạng đầu của dãy số là: \(2;\frac{9}{4};\frac{{64}}{{27}};\frac{{625}}{{256}};\frac{{7776}}{{3125}}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) 5 số hạng đầu của dãy số là: 1; 2; 6; 24; 120.
b) \({F_1} = 1,\;{F_2} = 1,\;{F_3} = 2,\;{F_4} = 3,\;{F_5} = 5\;\).
CM
21 tháng 9 2019
a. Năm số hạng đầu của dãy số
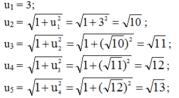
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
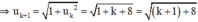
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \({u_n} = 3n - 2\)
\( \Rightarrow {u_1} = 3.1 - 2 = 1\)
\( \Rightarrow {u_2} = 3.2 - 2 = 4\)
\( \Rightarrow {u_3} = 3.3 - 2 = 7\)
\( \Rightarrow {u_4} = 3.4 - 2 = 10\)
\( \Rightarrow {u_5} = 3.5 - 2 = 13\)
\( \Rightarrow {u_{100}} = 3.100 - 2 = 298\)
b) \({u_n} = {3.2^n}\)
\( \Rightarrow {u_1} = {3.2^1} = 6\)
\( \Rightarrow {u_2} = {3.2^2} = 12\)
\( \Rightarrow {u_3} = {3.2^3} = 24\)
\( \Rightarrow {u_4} = {3.2^4} = 48\)
\( \Rightarrow {u_5} = {3.2^5} = 96\)
\( \Rightarrow {u_{100}} = {3.2^{100}}\)
c) \({u_n} = {\left( {1 + \frac{1}{n}} \right)^n}\)
\( \Rightarrow {u_1} = {\left( {1 + \frac{1}{1}} \right)^1} = 2\)
\( \Rightarrow {u_2} = {\left( {1 + \frac{1}{2}} \right)^2} = \frac{9}{4}\)
\( \Rightarrow {u_3} = {\left( {1 + \frac{1}{3}} \right)^3} = \frac{{64}}{{27}}\)
\( \Rightarrow {u_4} = {\left( {1 + \frac{1}{4}} \right)^4} = \frac{{625}}{{256}}\)
\( \Rightarrow {u_5} = {\left( {1 + \frac{1}{5}} \right)^5} = \frac{{7776}}{{3125}}\)
\( \Rightarrow {u_{100}} = {\left( {1 + \frac{1}{{100}}} \right)^{100}} = {\left( {\frac{{101}}{{100}}} \right)^{100}}\)