Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
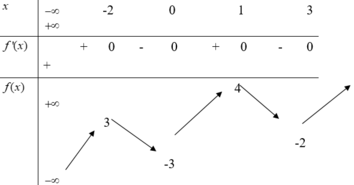
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
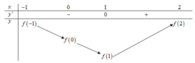
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()

\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)

Chọn A
Ta có: ![]()
![]()
![]()
![]()
![]()
![]()
Với ![]() nên f(x) đồng biến trên
ℝ
nên f(x) đồng biến trên
ℝ
Với ![]() nên f(x) nghich biến trên
ℝ
nên f(x) nghich biến trên
ℝ
Suy ra: ![]() Vì f(x) nghich biến trên
ℝ
nên
Vì f(x) nghich biến trên
ℝ
nên 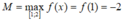 và
và ![]()
Từ đây ,ta suy ra: ![]()
=> chọn đáp án A
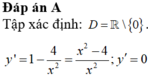
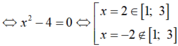
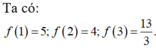
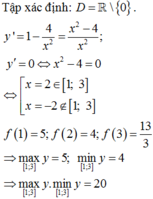


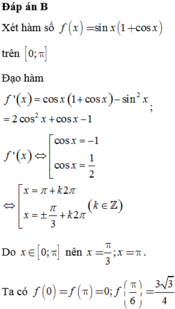
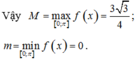
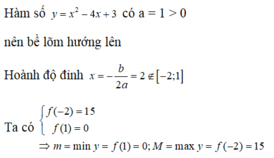
Đáp án B
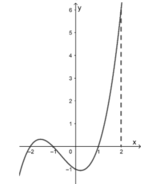
Ta có: f ' x = 1 − 1 x 2 = x 2 − 1 x 2 ≥ 0 ∀ x ∈ 1 ; 4 do đó hàm số đồng biến trên đoạn 1 ; 4
Do đó M i n 1 ; 4 f x . M ax 1 ; 4 f x = f 1 . f 4 = 17 2 .