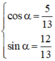Giải phương trình sau: 5cos2x + 12sin2x - 13 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2017
a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).
22 tháng 6 2016
a) cosx - √3sinx = √2 ⇔ cosx - tan
sinx = √2
⇔ coscosx - sinsinx = √2cos ⇔ cos(x + ) = 
⇔ 
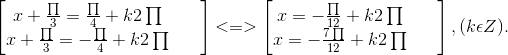
b) 3sin3x - 4cos3x = 5 ⇔ 
sin3x - 
cos3x = 1.
Đặt α = arccos thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = 
+ k2π
⇔ x = 
, k ∈ Z (trong đó α = arccos).
c) Ta có sinx + cosx = √2cos(x - 
) nên phương trình tương đương với
2√2cos(x - ) - √2 = 0 ⇔ cos(x - ) = 
⇔ 
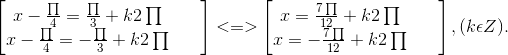
d) 5cos2x + 12sin2x -13 = 0 ⇔ 
Đặt α = arccos
thì phương trình trở thành
cosαcos2x + sinαsin2x = 1 ⇔ cos(2x - α) = 1
⇔ x = 
+ kπ, k ∈ Z (trong đó α = arccos).
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2020
c/
\(\Leftrightarrow\frac{5}{13}cos2x+\frac{12}{13}sin2x=1\)
Đặt \(\frac{12}{13}=cosa\) với \(a\in\left(0;\pi\right)\Rightarrow\frac{5}{13}=sina\)
Pt trở thành:
\(sin2x.cosa+cos2x.sina=1\)
\(\Leftrightarrow sin\left(2x+a\right)=1\)
\(\Leftrightarrow2x+a=\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\frac{a}{2}+\frac{\pi}{4}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2020
a/ Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^2x\)
\(2tan^2x+tanx-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=-\frac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=arctan\left(-\frac{3}{2}\right)+k\pi\end{matrix}\right.\)
b/ \(\Leftrightarrow\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=cos\frac{\pi}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{3}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{3}=-\frac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{12}+k2\pi\\x=-\frac{7\pi}{12}+k2\pi\end{matrix}\right.\)
NK
1
AH
Akai Haruma
Giáo viên
19 tháng 12 2017
Lời giải:
Đặt \(2x=t\Rightarrow y=5\cos t-12\sin t\)
\(\Rightarrow y'=-5\sin t-12\cos t=0\Leftrightarrow -5\sin t=12\cos t\)
Kết hợp với \(\sin ^2t+\cos ^2t=1\) ta suy ra \(y'=0\) khi
\((\sin t, \cos t)=(\frac{-12}{13}; \frac{5}{13})\) hoặc \((\sin t, \cos t)=(\frac{12}{13}; \frac{-5}{13})\)
Thử hai giá trị trên vào ta thấy \(y_{\min}=-13\) khi \((\sin t, \cos t)=(\frac{12}{13}; \frac{-5}{13})\)
Đáp án D
PT
1
CM
23 tháng 4 2017
Điều kiện của phương trình: sinx ≠ 0, cos ≠ 0, tan ≠ -1.
Biến đổi tương đương đã cho, ta được
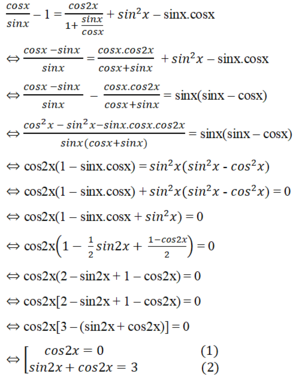
Phương trình (2) vô nghiệm vì |sin2x + cos2x| ≥ √2.
Phương trình (1) có nghiệm 2x = π/2+kπ,k ∈ Z
⇒ x = π/4+ k π/2,k ∈ Z.
Giá trị x = π/4+ k π/2, k = 2n + 1,
với n ∈ Z bị loại do điều kiện tanx ≠ -1.
CM
7 tháng 12 2019
Đáp án C
2 c os 2 2 x + 5 c os 2 x − 3 = 0 ⇔ c os 2 x = 1 2 ; hoặc c os 2 x = − 3 l o a i , c os 2 x = 1 2 ⇔ x = ± π 6 + k π .
Do x ∈ 0 ; 2 π . Vậy tổng các nghiệm của phương trình trong khoảng 0 ; 2 π là: S = π 6 + 7 π 6 + 5 π 6 + 11 π 6 = 4 π
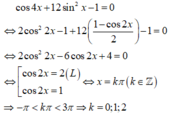
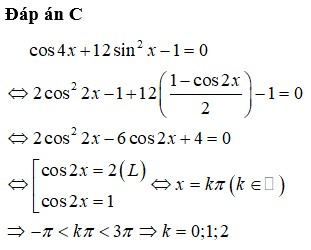
Vì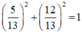
nên tồn tại α thỏa mãn
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
Vậy phương trình có họ nghiệm
với α thỏa mãn