Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn AB. Gọi M là trung điểm của SC. Giao điểm của BC với mp(ADM) là:
A. giao điểm của BC và AM
B. giao điểm của BC và SD
C. giao điểm của BC và AD
D. giao điểm của BC và DM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Gọi \(O=AC\cap BD\)
\(AM\in\left(SAC\right)\)
Mà \(\left(SAC\right)\cap\left(SBD\right)=SO\)
\(\Rightarrow J=AM\cap SO\)
Qua M kẻ \(d//AB\Rightarrow N=d\cap SD\)

Gọi E là giao điểm AB và CD
\(\Rightarrow E=\left(SAB\right)\cap\left(SCD\right)\)
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
b.
Do M là trung điểm SC, N là trung điểm BC
\(\Rightarrow MN\) là đường trung bình tam giác SBC
\(\Rightarrow MN||SB\)
Mà \(SB\in\left(SBD\right)\Rightarrow MN||\left(SBD\right)\)
c.
Trong mp (ABCD), nối AN cắt CD kéo dài tại F
Trong mp (SCD), nối FM kéo dài cắt SD tại G
\(\Rightarrow G=SD\cap\left(AMN\right)\)

a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
b: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
c: Chọn mp(SCD) có chứa CD
\(N\in SC\subset\left(SCD\right)\)
\(P\in SD\subset\left(SCD\right)\)
Do đó: \(NP\subset\left(SCD\right)\)
mà \(NP\subset\left(MNP\right)\)
nên (SCD) giao (MNP)=NP
Gọi E là giao điểm của CD với NP
=>E là giao điểm của CD với (MNP)
Chọn mp(SBD) có chứa MP
\(BD\subset\left(SBD\right)\)
\(BD\subset\left(ABCD\right)\)
Do đó: \(BD\subset\left(SBD\right)\cap\left(ABCD\right)\)
Gọi F là giao điểm của MP với BD
=>F là giao điểm của MP với (ABCD)

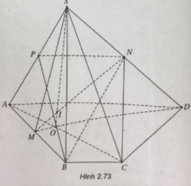
(h.2.73) a) Gọi O = AC ∩ MD Trong mặt phẳng (SMB) gọi I = SO ∩ MN.
Ta có: I = (SAC) ∩ MN
b) AD // BC (BC ⊂ (SBC))
⇒ AD // (SBC). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến NP // AD (P ∈ SA). Ta có thiết diện cần tìm là hình thang BCNP.
Đáp án C
Dễ thấy các cặp đường thẳng BC và AM, BC và SD, BC và DM là các cặp đường thẳng chéo nhau nên chúng không cắt nhau. Theo giả thiết, BC và AD cắt nhau. Ta gọi F là giao điểm của BC và AD.
Do F ∈ A D nên F ∈ A D M , từ đó suy ra F là giao điểm của đường thẳng BC và mặt phẳng (ADM).