Biết (với a là số hữu tỉ, b, c là các số nguyên dương và là phân số tối giản). Tính giá trị của
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

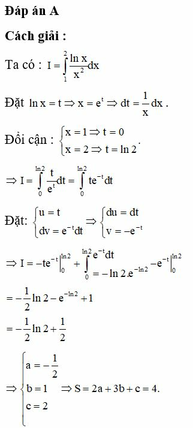

Một họ gồm m phần tử đại diện cho m lớp tương đương nói trên được gọi là một hệ thặng dư đầy đủ modulo m. Nói cách khác, hệ thặng dư đầy đủ modulo m là tập hợp gồm m số nguyên đôi một không đồng dư với nhau theo môđun m.
(x1, x2, …, xm) là hệ thặng dư đầy đủ modulo m ó xi – xj không chia hết cho m với mọi 1 £ i < j £ m.
Ví dụ với m = 5 thì (0, 1, 2, 3, 4), (4, 5, 6, 7, 8), (0, 3, 6, 9, 12) là các hệ thặng dư đầy đủ modulo 5.
Từ định nghĩa trên, ta dễ dàng suy ra tính chất đơn giản nhưng rất quan trọng sau:
Tính chất 1: Nếu (x1, x2, …, xm) là một hệ thặng dư đầy đủ modulo m thì
a) Với a là số nguyên bất kỳ (x1+a, x2+a, …, xm+a) cũng là một hệ thặng dư đầy đủ modulo m.
b) Nếu (a, m) = 1 thì (ax1, ax2, …, axm) cũng là một hệ thặng dư đầy đủ modulo m.
Với số nguyên dương m > 1, gọi j(m) là số các số nguyên dương nhỏ hơn m và nguyên tố cùng nhau với m. Khi đó, từ một hệ thặng dư đầy đủ mô-đun m, có đúng j(m) phần tử nguyên tố cùng nhau với m. Ta nói các phần tử này lập thành một hệ thặng dư thu gọn modulo m. Nói cách khác
(x1, x2, …, xj(m)) là hệ thặng dư thu gọn modulo m ó (xi, m) = 1 và xi – xj không chia hết cho m với mọi 1 £ i < j £ j(m).
Ta có
Tính chất 2: (x1, x2, …, xj(m)) là hệ thặng dư thu gọn modulo m và (a, m) = 1 thì
(ax1,a x2, …, axj(m)) cũng là một hệ thặng dư thu gọn modulo m.
Định lý Wilson. Số nguyên dương p > 1 là số nguyên tố khi và chỉ khi (p-1)! + 1 chia hết cho p.
Chứng minh. Nếu p là hợp số, p = s.t với s, t > 1 thì s £ p-1. Suy ra (p-1)! chia hết cho s, suy ra (p-1)! + 1 không chia hết cho s, từ đó (p-1)! + 1 không chia hết cho p. Vậy nếu (p-1)! + 1 chia hết cho p thì p phải là số nguyên tố.
~Hok tốt`
P/s:Ko chắc
\(a< b< c< d< e< f\)
\(\Rightarrow a+c+e< b+d+f\)
\(\Rightarrow2\left(a+c+e\right)< a+b+c+d+e+f\)
\(\Rightarrow\frac{a+c+e}{a+b+c+d+e+f}< \frac{1}{2}\)

Mình làm mẫu 2 bài đầu tiên thôi nhé!! 😃
a, Để 3/(x - 1) dương thì 3 và x - 1 cùng dấu
Mà 3 > 0 => x - 1 > 0 => x > 1
b, Để 5/(x - 2) âm thì 5 và x - 2 trái dấu
Mà 5 > 0 => x - 2 < 0 => x < 2
*tk giúp mình nhé!! 😊*
a, \(\frac{3}{x-1}\) là số dương => \(\frac{3}{x-1}>0\) => x - 1 cùng dấu với 3
Vì x - 1 là mẫu số \(\Rightarrow x-1\ne0\) \(\Rightarrow x-1>0\Rightarrow x>0+1\Rightarrow x>1\)
b, \(\frac{5}{x-2}\) là số âm => \(\frac{5}{x-2}< 0\) => x - 2 khác dấu với 5
Vì x - 2 là mẫu số \(\Rightarrow x-2\ne0\Rightarrow x-2< 0\Rightarrow x< 0+2\Rightarrow x< 2\)
c, \(\frac{x-3}{x-5}\) là số dương => \(\frac{x-3}{x-5}>0\) => x - 3 và x - 5 cùng dấu
\(TH1:\hept{\begin{cases}x-3>0\\x-5>0\end{cases}\Rightarrow\hept{\begin{cases}x>0+3\\x>0+5\end{cases}\Rightarrow\hept{\begin{cases}x>3\\x>5\end{cases}\Rightarrow}}x>5}\)
\(TH2:\hept{\begin{cases}x-3< 0\\x-5< 0\end{cases}\Rightarrow}\hept{\begin{cases}x< 0+3\\x< 0+5\end{cases}\Rightarrow\hept{\begin{cases}x< 3\\x< 5\end{cases}\Rightarrow}x< 3}\)
d, \(\frac{x+7}{x+10}\) là số âm => \(\frac{x+7}{x+10}< 0\) => x + 7 và x + 10 khác dấu
\(TH1:\hept{\begin{cases}x+7>0\\x+10< 0\end{cases}\Rightarrow}\hept{\begin{cases}x>0-7\\x< 0-10\end{cases}\Rightarrow}\frac{x>-7}{x< -10}\) ( loại )
\(TH2:\hept{\begin{cases}x+7< 0\\x+10>0\end{cases}\Rightarrow\hept{\begin{cases}x< 0-7\\x>0-10\end{cases}\Rightarrow}\hept{\begin{cases}x< -7\\x>-10\end{cases}\Rightarrow}-10< x< -7}\)

a) \(\dfrac{-5}{a-3}\left(a\inℤ\right)\) là số hữu tỷ \(\Leftrightarrow a-3\ne0\Leftrightarrow a\ne3\)
b) \(\dfrac{-5}{a-3}\left(a\inℤ\right)\) là số hữu tỷ dương \(\Leftrightarrow a-3< 0\Leftrightarrow a< 3\)
c) \(\dfrac{-5}{a-3}\left(a\inℤ\right)\) là số hữu âm \(\Leftrightarrow a-3>0\Leftrightarrow a>3\)
d) \(\dfrac{-5}{a-3}\left(a\inℤ\right)\) là số nguyên đương
\(\Leftrightarrow a-3\in B\left(5\right)=\left\{-1;-5\right\}\)
\(\Leftrightarrow a\in\left\{2;-2\right\}\)
a) để x là số nguyên dương thì : a - 3 / 2 > 0
suy ra: a > 3 / 2
b) để x là số nguyên âm thì : a - 3 / 2 < 0
suy ra: a < 3 / 2
c) x ko là số dương , ko là số âm tức là x = 0
suy ra a= 3/2
nếu đúng thì cho mk nha
chúc bn hk giỏi