Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy ABCD. Góc giữa SC và mặt đáy bằng 45 ° . Gọi E là trung điểm BC. Tính khoảng cách giữa hai đường thẳng DE và SC
A. a 38 19
B. a 5 5
C. a 38 5
D. a 5 19
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
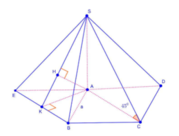
Góc giữa SC và mặt đáy bằng 45 o ⇒ S C A ^ = 45 o
Xét tam giác SAC vuông tại A, ta có
![]()
Dựng hình bình hành ACBE
![]()
Gọi H là hình chiếu của A lên mặt phẳng (SBE).
![]()
![]()
Xét hình tứ diện vuông SABE có
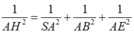
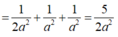
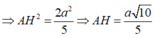

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

Đáp án A
Gắn trục tọa độ Axyz với A là gốc tọa độ sao cho:
Tia Ax trùng tia AB; tia Ay trùng tia AD; tia Az trùng tia AS.
Khi đó:
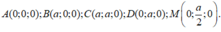
Gọi O là tâm hình vuông ABCD.
Do góc giữa mặt phẳng(SBD)và (ABCD) bằng 60 o nên S O A ⏞ = 60 o
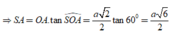
⇒ S 0 ; 0 ; a 6 2
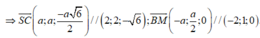
Mặt phẳng (P) chứa SC và song song với BM có vecto pháp tuyến là ( 6 ; 2 6 ; 6 ) / / 1 ; 2 ; 6 nên có phương trình:
x + 2 y + 6 z - 3 a = 0
Do đó: d ( S C , B M ) = d ( B ; ( P ) ) = 2 a 11 (đvđd).


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
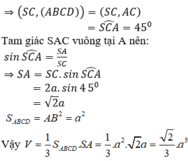
Chọn A