Có năm đoạn thẳng có độ dài lần lượt là 1 c m , 2 c m , 3 c m , 4 c m , 5 c m . Lấy ngẫu nhiên ra ba đoạn thẳng, tính xác suất để ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam giác
A. 1 10 .
B. 3 10 .
C. 2 5 .
D. 3 5 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Lấy ba đoạn thẳng từ năm đoạn thẳng có
C
5
3
= 10 cách. Suy ra số phần tử của không gian mẫu là ![]()
Gọi A là biến cố: " Ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác ".
Khi đó 3 đoạn thẳng được chọn thỏa mãn tính chất: Tổng độ dài 2 đoạn thẳng luôn lớn hơn độ dài đoạn thẳng còn lại.
Có 3 bộ thỏa mãn là ![]()
Vậy xác suất để ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác là
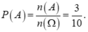

Ta có: \(MB=\frac{AB}{2}=\frac{4}{2}=2\left(cm\right)\)
Và \(BN=\frac{BC}{2}=\frac{2}{2}=1\left(cm\right)\)
Suy ra: \(MN=MB+BN=2+1=3\left(cm\right)\)
Vậy \(MN=3cm\)
hok tốt!!
ta có:
do M là trung điểm của AB nên AM=MB=\(\frac{AB}{2}\)=2cm
do n là trung điểm của BC nên BN=NC=\(\frac{BC}{2}\)=1CM
đoạn thẳng MN dài là : 2+1=3cm