Biết M 2 ; − 1 , N 3 ; 2 lần lượt là hai điểm biểu diễn cho số phức z 1 , z 2 trên mặt phẳng tọa độ phức O x y . Khi đó môđun của số phức z 1 2 + z 2 bằng
A. 4 2 .
B. 2 10 .
C. 10 .
D. 68 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

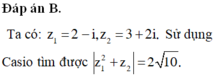

\(a,M\left(-2;2\right)\in\left(d\right)\Leftrightarrow-2\left(m-2\right)+1=2\Leftrightarrow m=\dfrac{3}{2}\\ b,N\left(-3;4\right)\in\left(d\right)\Leftrightarrow-3\left(m-2\right)+1=4\Leftrightarrow m=1\\ c,\left(d\right)\cap Ox=\left(5;0\right)\Leftrightarrow5\left(m-2\right)+1=0\Leftrightarrow m=\dfrac{9}{5}\\ d,\left(d\right)\cap Oy=\left(0;-2\right)\Leftrightarrow1=-2\Leftrightarrow m\in\varnothing\\ e,\left(d\right)//\left(d'\right)\Leftrightarrow m-2=3\Leftrightarrow m=5\)

1.
Ta thấy $(x-13)^2\geq 0$ với mọi $x$
$\Rightarrow T=(x-13)^2-26\geq 0-26=-26$
Vậy GTNN của $T$ là $-26$.
Giá trị này đạt tại $x-13=0\Leftrightarrow x=13$
2.
Ta thấy: $(x-14)^2\geq 0$ với mọi $x$
$\Rightarrow M=20-(x-14)^2\leq 20-0=20$
Vậy $M_{\max}=20$. Giá trị này đạt tại $x-14=0$
Hay $x=14$.

a) Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(\left|x-1\right|+\left|x+3\right|=\left|1-x\right|+\left|x+3\right|\ge\left|1-x+x+3\right|=4\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}1-x\ge0\\x+3\ge0\end{matrix}\right.\)
\(\Leftrightarrow-3\le x\le1\)
Vậy,..................................................................................................................................

m2 + n2 + 2 = 2.(m+n) => (m2 - 2m + 1) + (n2 - 2n + 1) = 0
=> (m - 1)2 + (n - 1)2 = 0 Mà (m -1)2 và (n -1)2 đều lớn hơn hoặc bằng 0
=> m - 1= n - 1 = 0 => m = n = 1
Bài làm
m2 + n2 + 2
= 2.(m+n)
=> (m2 - 2m + 1) + (n2 - 2n + 1)
= 0
=> (m - 1)2 + (n - 1)2 = 0 Mà (m -1)2 và (n -1)2 \(\ge\) 0
=> m - 1= n - 1 = 0
=> m = n = 1
hok tốt

2^m+2^n=2^(m+n)=2^m*2^n
thế này nhé
chuyển vế
2^m-2^m*2^n+2^n-1=-1
(2^m-1)(2^n-1)=1
do m,n là số tự nhiên nên 2^m-1 và 2^n-1 là ước dương của 1
hay đồng thời xảy ra 2^m-1=1 và 2^n-1=1 suy ra m=n=1

Bài 2:
a: =>5 căn m=căn 3
=>căn m=căn 3/5
=>m=3/25
b: =>144(n-2)=362
=>(n-2)=9
=>n=11

Ta có :
2m + 2n = 2m + n
2m + 2n = 2m . 2n
2m . 2n - 2m - 2n = 0
2m . ( 2n - 1 ) - 2n + 1 - 1 = 0
2m . ( 2n - 1 ) - ( 2n - 1 ) = 0 + 1
( 2m - 1 ) . ( 2n - 1 ) = 1 = 1 . 1
2m - 1 = 1
=> 2m = 2 => m = 1
2n - 1 = 1 => 2n = 2 => n = 1
Vậy m = 1 ; n = 1

Bài 3:
=>2xy-x-y-2=0
=>x(2y-1)-y+0,5-2,5=0
=>x(2y-1)-(y-0,5)=2,5
=>2x(2y-1)-(2y-1)=5
=>(2y-1)(2x-1)=5
=>\(\left(2x-1;2y-1\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(0;-2\right);\left(-2;0\right)\right\}\)
Câu 5:
Đặt x/2=y/3=z/4=k
=>x=2k; y=3k; z=4k
x^2+y^2+z^2=116
=>4k^2+9k^2+16k^2=116
=>29k^2=116
=>k^2=4
TH1: k=2
=>x=4; y=6; z=8
TH2: k=-2
=>x=-4; y=-6; z=-8

a)
\(A=\dfrac{2x^2-16x+41}{x^2-8x+22}=\dfrac{2\left(x^2-8x+22\right)-3}{x^2-8x+22}\)
\(A-2=-\dfrac{3}{x^2-8x+22}=-\dfrac{3}{\left(x-4\right)^2+6}\ge-\dfrac{3}{6}=-\dfrac{1}{2}\)
\(A\ge\dfrac{3}{2}\) khi x =4