Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = 3 a , B C = 4 a và S A ⊥ A B C . Góc giữa đường thẳng SC và mặt phẳng A B C bằng 60 ° . Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
A. 10 3 a 79
B. 5 a 2
C. 5 3 a
D. 5 3 a 79

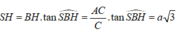
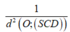
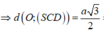




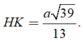
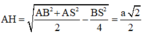
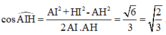

Đáp án A
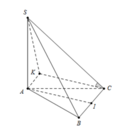
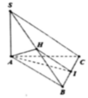
Do S A ⊥ A B C nên góc giữ SC và A B C là góc S C A ^ = 60 °
Vì Δ A B C vuông tại B nên A C = 5 a ⇒ S A = 5 a 3
Gọi N là trung điểm BC nên M N / / A B ⇒ A B / / S M N
d A B , S M = d A B , S M N = d A , S M N .
Từ A kẻ đường thẳng song song vơi BC cắt MN tại D.
Do B C ⊥ A B ⇒ B C ⊥ M N ⇒ A D ⊥ M N .
Từ A kẻ AH vuông góc vơi SD
Ta có M D ⊥ A D M D ⊥ S A ⇒ M D ⊥ S A D ⇒ M D ⊥ A H
Mà A H ⊥ S D ⇒ A H ⊥ S M D hay A H ⊥ s m n ⇒ d A , S M N = A H
Do A D = B N = 1 2 B C = 2 a .
Xét Δ S A D có 1 A H 2 = 1 S A 2 + 1 A D 2 = 1 75 a 2 + 1 4 a 2 = 79 300 a 2
⇒ d A B , S M = A H = 10 237 a 79 = 10 3 a 79