Cho Δ A B C có A ^ = 60 0 có AD là đường phân giác. Từ điểm E bất kỳ thuộc AC vẽ một tia song song với AD cắt BC ở K.
a) Tính C A D ^
b) Tính C E K ^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2017
a/ ta có A=60 mà AD là tia phân giác
=> CAD= 1/2 A = 1/2.60= 30
b/ ta có CEK=CAD ( 2 góc đồng vị, EK//AD)
=> CEK= 30
22 tháng 7 2017
mình ko biết vẽ hình trên này bạn tự vẽ đi
ta có:
ME//AD suy ra \(\hept{\begin{cases}DAF=AFE\left(soletrong\right)\\DAC=AEF\left(dongvi\right)\end{cases}}\) mà \(DAC=DAF\) vì AD là phân giác góc A
\(\Rightarrow AEF=AFE\)
4 tháng 8 2019
a) Vì AD là phân giác BAC
=> BAD = CAD = \(\frac{60°}{2}\)= 30°
Vì AB//DM
=> BAD = ADM = 30° ( so le trong)
Vì AD//MK
=> ADM = DMK = 30° ( so le trong)
b) Mà AD//MK
=> DAC = KMC = 30° ( đồng vị)
=> DMK = KMC = 30°
Hay MK là phân giác DMC
KV
4 tháng 12 2023
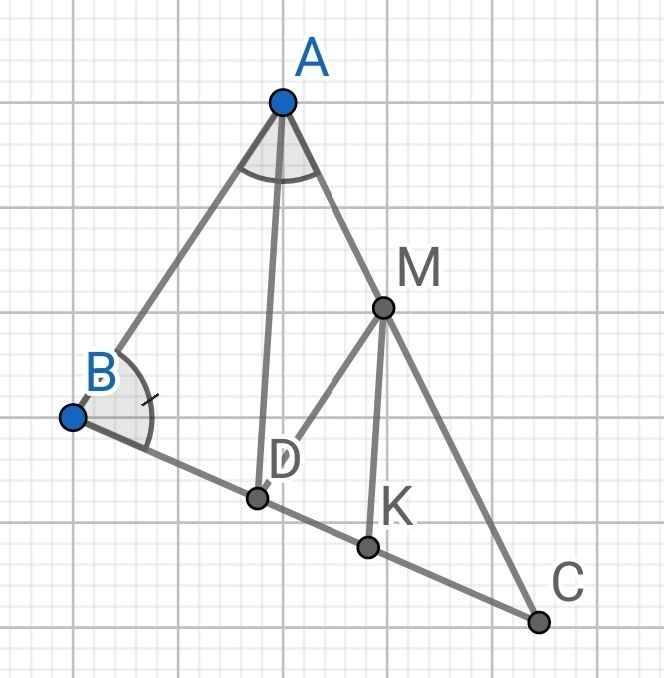
Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠DAM = 60⁰ : 2 = 30⁰
Do DM // AB (gt)
⇒ ∠ADM = ∠BAD = 30⁰ (so le trong)
Do DM // AB (gt)
⇒ ∠MDK = ∠B = 80⁰ (đồng vị)
⇒ ∠ADK = ∠ADM + ∠MDK
= 30⁰ + 80⁰
= 110⁰
30 tháng 9 2015
a) Vì AB// MD suy ra BAD= MDA (so le) ; AD// MK suy ra ADM= KDM (so le)
nên BAD= ADM= DMK
b) Vì BAD= DMK (câu a) mà BAD= KMC (đồng vị vì AD// MC)
nên DMK= CMK suy ra MK là phân giác DMC
tích đúng cho mình nhé
a) C A D ^ = C A B ^ 2 = 60 0 2 = 30 0 (AD là tia phân giác)
b) C E K ^ = C A D ^ = 30 0 (cặp góc đồng vị; EK // AD)