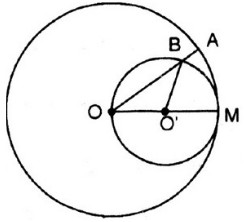
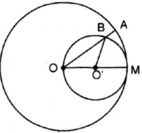
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
Chứng minh cung Ma và cung MB có độ dài bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB

Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB

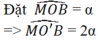 (góc nội tiếp và góc ở tâ của đường tròn (O'))
(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
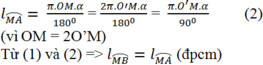

Xét (\(\dfrac{MO}{2}\)) có
ΔOAM nội tiếp đường tròn
OM là đường kính
Do đó: ΔOAM vuông tại A
hay MA là tiếp tuyến có A là tiếp điểm của (O)
Xét \(\left(\dfrac{OM}{2}\right)\) có
ΔOBM nội tiếp đường tròn
OM là đường kính
Do đó: ΔOBM vuông tại B
hay MB là tiếp tuyến có B là tiếp điểm của (O)

a. b.
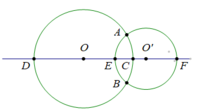
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm
Kiến thức áp dụng
+ Trên đường tròn đường kính R, độ dài cung n0 bằng :