Có 2 học sinh lớp A, 3 học sinh lớp B và 4 học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh lớp B. Hỏi có bao nhiêu cách xếp hàng như vậy?
A. 80640
B. 108864
C. 145152
D. 217728
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 2 2017
Đáp án C
Phương pháp:
Sử dụng quy tắc vách ngăn.
Cách giải:
Xếp 2 học sinh lớp A có 2! cách xếp, khi đó tạo ra 3 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ nhất vào 1 trong 2 khoảng trống không ở giữa 2 bạn lớp A có 2 cách, khi đó tạo ra 4 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ 2 vào 1 trong 3 khoảng trống không ở giữa 2 bạn lớp A có 3 cách, khi đó tạo ra 5 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ 3 vào 1 trong 4 khoảng trống không ở giữa 2 bạn lớp A có 4 cách, khi đó tạo ra 6 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp C thứ nhất vào 1 trong 6 khoảng trống (kể cả khoảng trống giữa 2 bạn lớp A) có 6 cách, khi đó tạo ra 7 khoảng trống.
Cứ như vậy ta có :
Xếp bạn lớp C thứ hai có 7 cách.
Xếp bạn lớp C thứ ba có 8 cách.
Xếp bạn lớp C thứ tư có 9 cách.
Vậy số cách xếp 9 học sinh trên thỏa mãn yêu cầu là 2!.2.3.4.5.6.7.8.9 = 145152 cách.
CM
18 tháng 1 2019
Xếp 2 học sinh lớp A có 2! cách xếp, khi đó tạo ra 3 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ nhất vào 1 trong 2 khoảng trống không ở giữa 2 bạn lớp A có 2 cách, khi đó tạo ra 4 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ 2 vào 1 trong 3 khoảng trống không ở giữa 2 bạn lớp A có 3 cách, khi đó tạo ra 5 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp B thứ 3 vào 1 trong 4 khoảng trống không ở giữa 2 bạn lớp A có 4 cách, khi đó tạo ra 6 khoảng trống trong đó có 1 khoảng trống giữa 2 bạn lớp A.
Xếp bạn lớp C thứ nhất vào 1 trong 6 khoảng trống (kể cả khoảng trống giữa 2 bạn lớp A) có 6 cách, khi đó tạo ra 7 khoảng trống.
Cứ như vậy ta có :
Xếp bạn lớp C thứ hai có 7 cách.
Xếp bạn lớp C thứ ba có 8 cách.
Xếp bạn lớp C thứ tư có 9 cách.
Vậy số cách xếp 9 học sinh trên thỏa mãn yêu cầu là 2!.2.3.4.5.6.7.8.9=145152 cách.
Chọn đáp án C.
CM
29 tháng 8 2018
Chọn C
Để xếp 9 em học sinh thành một hàng dọc ta thực hiện ba hành động liên tiếp
* Sắp xếp 3 học sinh lớp B. Có 3! cách.
* Sắp xếp 2 học sinh lớp A đứng cạnh các học sinh lớp B sao cho giữa hai học sinh lớp A không có học sinh lớp B. Có A 4 1 .2! cách.
* Lần lượt sắp xếp 4 học sinh lớp C còn lại đứng cạnh các học sinh trên. Có A 9 4 cách.
Vậy có tất cả 3! A 4 1 .2!. A 9 4
Bình luận: Trong đề thi thử THPT chuyên Thái Nguyên lần 2 trong câu hỏi này không có đáp án 145152 mà thay bởi đáp án 145112. Tôi thiết nghĩ lỗi do người làm đề đã đánh máy nên đã tự ý đổi lại một đáp án khác mà tôi nghĩ chính xác hơn.
CM
25 tháng 11 2019
Đáp án C
Số cách xếp ngẫu nhiên là 10! cách.=
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn k ∈ 0 , 1 , 2 , 3 , 4 , 5 học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có A 5 k cách, ta được một nhóm X.
* Xếp 10 - (2+k) = 8- k học sinh còn lại với nhóm X có (9 -k)! cách.
Vậy tất cả có ∑ 2 k = 0 5 ! A 5 k ( 9 - k ) ! = 1451520 cách xếp thỏa mãn
Xác suất cần tính bằng 1451520 10 ! = 2 5
CM
25 tháng 11 2019
Chọn C
Số cách xếp ngẫu nhiên là 10! cách.
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn 
học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có
A
5
k
cách, ta được một nhóm X.
* Xếp 
học sinh còn lại với nhóm X có (9-k)! cách.
Vậy tất cả có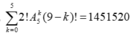 
cách xếp thỏa mãn.
Xác suất cần tính bằng 
Đáp án C
Gọi k là số học sinh lớp C ở giữa hai học sinh lớp A với k = 0 ; 1 ; 2 ; 3 ; 4
Chọn 2 học sinh lớp A xếp 2 đầu có 2 ! cách. Chọn k học sinh lớp C xếp vào giữa 2 học sinh lớp A có A 4 k cách. Vậy có 2 ! . A 4 k cách xếp để được hàng A C ... C A ⏟ k
Coi cụm A C ... C A ⏟ k là 1 vị trí cùng với 9 − k + 2 học sinh còn lại thành 8 − k vị trí.
Xếp hàng cho các vị trí này có 8 − k ! cách. Vậy với mỗi k như trên có 2 ! . A 4 k . 8 − k ! cách xếp.
Vậy tổng số cách xếp thỏa mãn đề bài là ∑ k = 0 4 2 ! . A 4 k . 8 − k ! = 145152 cách.