Trong không gian với hệ tọa độ Oxyz, cho điểm và mặt phẳng với m là tham số. Gọi điểm là hình chiếu vuông góc của điểm A trên Tính khi khoảng cách từ điểm A đến lớn nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Gọi điểm H là hình chiếu của A 4 ; 1 ; − 2 trên mặt phẳng O x z , khi đó H 4 ; 0 ; − 2 .
Điểm A' đối xứng với A 4 ; 1 ; − 2 qua mặt phẳng O x z nên H 4 ; 0 ; − 2 là trung điểm AA' . Khi đó A ' 2 x H − x A ; 2 y H − y A ; 2 z H − z A → A ' 4 ; − 1 ; − 2

Đáp án A
Dễ thấy tọa độ trung điểm của đoạn thẳng AB là điểm.

Đáp án A
Dễ thấy tọa độ trung điểm của đoạn thẳng AB là điểm

Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).

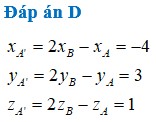

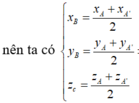
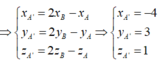
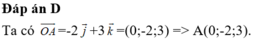
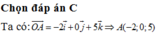
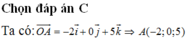
Đáp án D
Ta có
P : x + m y + 2 m + 1 z − 2 − m = 0 ⇔ x + z − 2 + m y + 2 z − 1 = 0
⇒ P luôn đi qua đường thẳng cố định
d : x + z − 2 = 0 y + 2 z − 1 = 0 . d A ; P m ax = d A ; d
Lại có
H ∈ d : x = 2 − t y = 1 − 2 t z = t ⇒ u → d = − 1 ; − 2 ; 1
và H 2 − t ; 1 − 2 t ; t .
Suy ra
A H → . u → d = 0 ⇔ t + 4 t + t − 3 = 0 ⇔ t = 1 2 .
Vậy H 3 2 ; 0 ; 1 2 .