Tìm số nguyên a, biết: |a| = |-8|
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 4 2019
a, x ∈ {-7;-6;-5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8}
b, (-7)+(-6)+(-5)+(-4)+(-3)+(-2)+(-1)+0+1+2+3+4+5+6+7+8
=[(-7)+7]+[(-6)+6]+[(-5)+5]+[(-4)+4]+[(-3)+3]+[(-2)+2]+[(-1)+1]+0+8
= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 8
= 8
VV
20 tháng 2 2021
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 8 9 còn câu B thì cộng mấy số này vào
PT
1
VT
1
28 tháng 1 2016
=>(a+3) là ước của -8 => thuộc (1;-1;2;-2;4;-4;8;-8)
Tự thử chọn bạn nhé
PH
1
20 tháng 8 2015
\(\frac{8}{17}<\frac{10}{a}=\frac{8}{11}\)
\(\frac{88a}{187a}<\frac{1870}{187a}<\frac{136a}{187a}\)
88a < 1870 < 136a
88 < 1870 : a < 136
Vì a là số nguyên tố nên a = 13
CM
6 tháng 7 2017
a, Do (a,b) = 6 => a = 6m; b = 6n với m,n ∈ N*; (m,n) = 1 và m ≤ n
Vì vậy ab = 6m.6n = 36mn, do ab = 216 => mn = 6. Do đó m = 1, n = 6 hoặc m = 2, n = 3
Với m = 1, n = 6 thì a = 6, b = 36
Với m = 2, n = 3 thì a = 12, b = 18
Vậy (a;b) là (6;36); (12;18)
b, Vì p là số nguyên tố nên ta xét các trường hợp của p
Trường hợp 1: p = 2, khi đó p+4 = 6; p+8 = 10 không là số nguyên tố (loại).
Trường hợp 2: p = 3, khi đó p+4 = 7; p+8 = 11 là hai số nguyên tố (thỏa mãn).
Trường hợp 3: p>3 nên p có dạng 3k+1; 3k+2 với k ∈ N*.
Nếu p = 3k+1 thì p+8 = 3k+1+8 = 3k+9 chia hết cho 3 và lớn hơn 3 nên p+8 không là số nguyên tố (loại).
Nếu p = 3k+2 thì p+4 = 3k+2+4 = 3k+6 chia hết cho 3 và lớn hơn 3 nên p+4 không là số nguyên tố (loại).
Kết luận. p = 3
DM
1
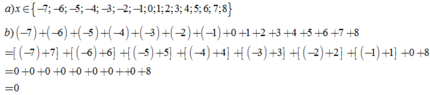
|a| = |-8| ⇒ |a| = 8
Suy ra a = 8 hoặc a = -8