Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ Olàm trực tâm
A. m=0
B. m=2
C. m=1
D. Không tồn tại m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
CM
5 tháng 2 2018
Chọn D
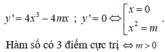
Khi đó đồ thị hàm số có 3 điểm cực trị là:
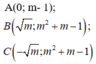
Vì B, C đối xứng với nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác:
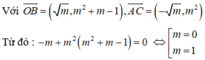
Kết hợp điều kiện, vậy m = 1 là giá trị cần tìm
CM
28 tháng 9 2018
+ Đạo hàm y’ = 4x3- 4mx
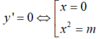
Hàm số có 3 điểm cực trị khi và chỉ khi m≠0.
+ Khi đó đồ thị hàm số có 3 điểm cực trị là:
+ Vì B,C đối xứng nhau qua trục tung nên BC và OA vuông góc với nhau.
Do đó O là trực tâm tam giác ABC khi và chỉ khi OB vuông góc AC hay 
Với
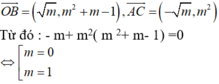
Kết hợp với điều kiện m ≠ 0 thì m = 1 là giá trị cần tìm.
Chọn B.
CM
29 tháng 8 2018
Chọn D
y ' = 4 x 3 - 4 m x
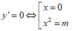
Hàm số có 3 điểm cực trị ⇔ m > 0
Khi đó đồ thị hàm số có 3 điểm cực trị là
A (0;m-1)
B ( m ; m 2 + m - 1 )
C ( - m ; m 2 + m - 1 )
Vì B,C đối xứng nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác ABC
Với O B ⇀ = ( m , m 2 + m - 1 ) , A C ⇀ = ( - m , m 2 )
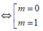
Vậy m = 1 là gtct
CM
6 tháng 6 2019
Đáp án D
Ta có y ' = 4 x 3 − 4 m x = 4 x x 2 − m .
Hàm số có 3 điểm cực trị ⇔ y ' = 0 có 3 nghiệm phân biệt, suy ra m > 0 1 .
Suy ra tọa độ 3 điểm cực trị của đồ thị hàm số là
A 0 ; 0 , B m ; − m 2 , C − m ; − m 2 ⇒ A B ¯ = m ; − m 2 A C ¯ = − m ; − m 2 B C ¯ = 2 m ; 0 .
Suy ra tam giác ABC cân tại A.
Gọi H 0 ; − m 2 là trung điểm của B C ⇒ A H ¯ = 0 ; − m 2 ⇒ A H = m 2 .
Suy ra S A B C = 1 2 A H . B C = 1 2 m 2 2 m 2 = m 4 < 1 ⇔ − 1 < m < 1 2 .
Từ (1), (2) ⇒ 0 < m < 1.
