Trong các khẳng định sau về hàm số y = − 2 x 4 + 4 x 2 − 1, khẳng định nào là SAI ?
A. Đồ thị của hàm số cắt trục Ox tại 2 điểm phân biệt
B. Hàm số có 3 điểm cực trị.
C. Hàm số có 2 điểm cực tiểu và 1 điểm cực đại.
D. Đồ thị của hàm số nhận Oy làm trục đối xứng

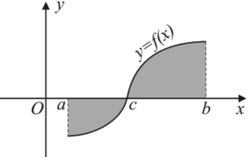
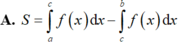
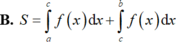
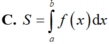
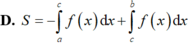
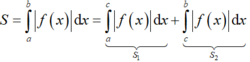
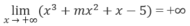
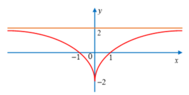
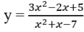
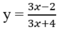 luôn nghịch biến;
luôn nghịch biến;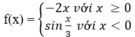
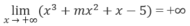

Đáp án C
Ta có
y ' = − 8 x 3 + 8 x = − 8 x ( x 2 − 1 ) ⇒ y ' = 0 ⇔ x = 0, y 0 = − 1 x = ± 1, y 0 = 1
Hàm số có hai điểm cực đại và một điểm cực tiểu.
Chọn phương án C.