Xét khối hộp chữ nhật ABCD.A’B’C’D’ có đáy ABCD là một hình vuông và diện tích toàn phần của hình hộp đó là 32. Thể tích lớn nhất của khối hộp ABCD.A’B’C’ là bao nhiêu?
A. V= 56 3 9
B. V= 70 3 9
C. V= 64 3 9
D. V= 80 3 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Thể tích của khối hộp chữ nhật có chiều cao bằng h, đáy là hình vuông cạnh a được tính theo công thức:
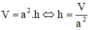 .
.
Diện tích toàn phần của hình hộp là:
![]()
![]()

Đáp án B
Ta có
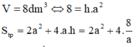
Ta tìm điều kiện của a đê diện tích toàn phần nhỏ nhất. xét hàm số ta được a=2
Đáp án C
Ta có diện tích toàn phần của hình hộp chữ nhật là S = 32 = 2 a 2 + 4 a b = 2 ( a 2 + a b + a b ) ≥ 2 . 3 a 2 . a b . a b 3 = 6 ( a 2 b ) 2 3 = 6 V 2 3
⇒ V 2 3 ≤ 32 6 ⇔ V ≤ ( 16 3 ) 3 = 64 3 9