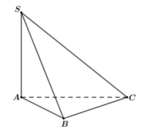
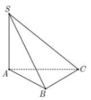
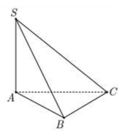
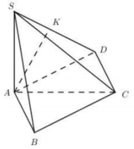
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , A B = 3 a , B C = 4 a . Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC với đáy bằng 60 ° . Gọi M là trung điểm AC, tính khoảng cách giữa hai đường thẳng AB và SM
A. a 3
B. 10 a 3 79
C. 5 a 2
D. 5 a 3

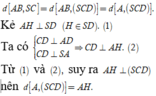

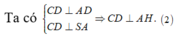
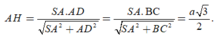
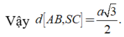
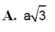
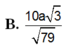
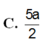
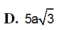
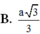
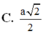
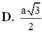


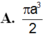
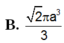

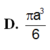
Đáp án B
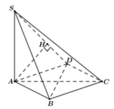
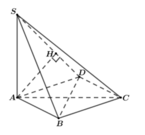
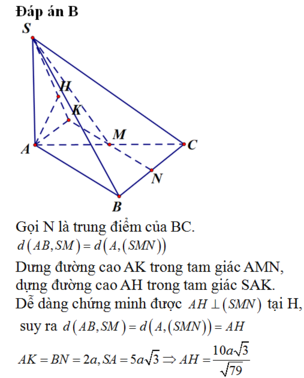
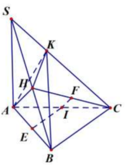
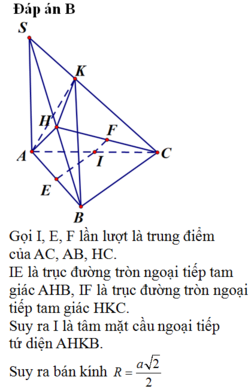
Gọi N là trung điểm của BC.
d A B , S M = d A , S M N
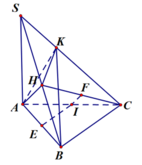
Dưng đường cao AK trong tam giác AMN, dựng đường cao AH trong tam giác SAK.
Dễ dàng chứng minh được A H ⊥ S M N tại H, suy ra d A B , S M = d A , S M N = A H
A K = B N = 2 a , S A = 5 a 3 ⇒ A H = 10 a 3 79