Cho hai hàm số: y = 2x – 3 và y = (-1/2)x + 2 có đồ thị lần lượt là các đường thẳng (d1) và (d2). a) Vẽ trên cùng một hệ trục tọa độ các đường thẳng (d1) và (d2). b) Tìm tọa độ giao điểm hai đường thẳng (d1) và (d2) bằng phép toán. c) Tính góc tạo bởi đường thẳng (d1) và trục Ox.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 3 2017
a, HS Tự làm
b, Tìm được C(–2; –3) là tọa độ giao điểm của d 1 và d 2
c, Kẻ OH ⊥ AB (CH ⊥ Ox)
S A B C = 1 2 C H . A B = 9 4 (đvdt)
16 tháng 11 2023
a: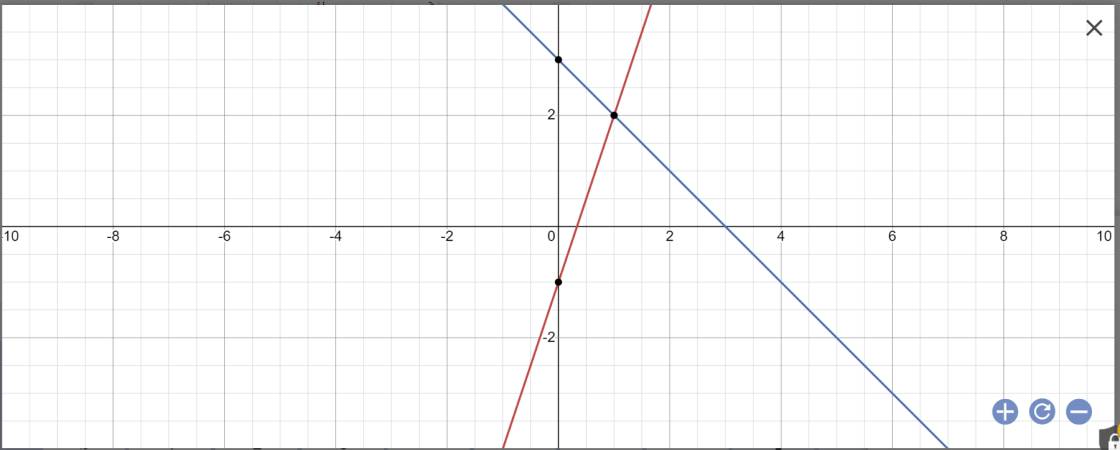 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
11 tháng 8 2021
b) Phương trình hoành độ giao điểm của (D1) và (d2) là:
-x+4=x-4
\(\Leftrightarrow-2x=-8\)
hay x=4
Thay x=4 vào (d1), ta được:
y=-4+4=0
Thay x=0 vào (d1), ta được:
\(y=-0+4=4\)
Thay x=0 vào (d2), ta được:
\(y=0-4=-4\)
Vậy: A(0;4); B(0;-4); C(4;0)
7 tháng 11 2021
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x=x-1\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
25 tháng 11 2023
a: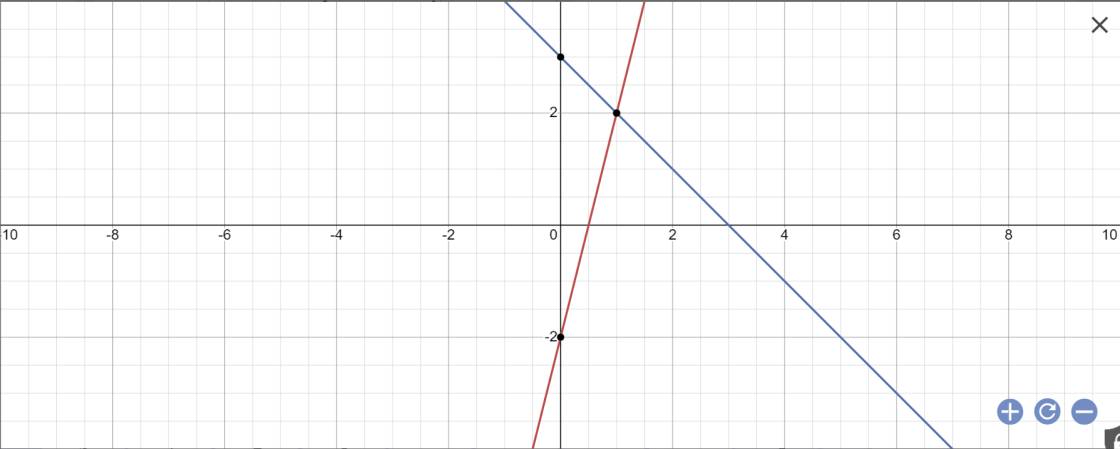 
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)
20 tháng 11 2021
\(b,\) PT hoành độ giao điểm: \(-2x+5=x+2\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow M\left(1;3\right)\)