Tìm tất cả các giá trị thực của tham số m để phương trình 2 x = m − 1 có nghiệm thực.
A. m ≥ 1
B. m ≠ 1
C. m>1
D. m>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 7 2018
Phương trình có hai nghiệm phân biệt ⇔ ∆ > 0
⇔ m 2 - 8 m + 16 = 0 m - 4 2 > 0 ⇔ m ≠ 4 *
Theo định lí Viet, ta có:
x 1 . x 2 = m − 1 3 ; x 1 + x 2 = m + 2 3 x 1 = 2 x 2 ⇔ x 1 = 2 9 ( m + 2 ) , x 2 = 1 9 ( m + 2 ) x 1 . x 2 = m − 1 3
⇒ 2 81 ( m + 2 ) 2 = m − 1 3 ⇔ 2 m 2 − 19 m + 35 = 0 ⇔ m = 5 2 m = 7 (thỏa mãn (*))
Đáp án cần chọn là: A
CM
30 tháng 10 2017
Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
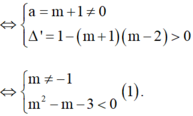
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
CM
22 tháng 5 2017
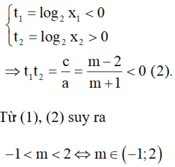
Đáp án C
Phương pháp:
phương trình trở thành
=> Hàm số đồng biến trên khoảng [2;+∞)
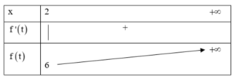
Để phương trình (*) có nghiệm thì 2m ≥ 6 ⇔ m ≥ 3
CM
21 tháng 5 2019
Chọn B.
Phương trình đã cho tương đương : 22x-1 = - m2 + m
Vì 2x - 1 có miền giá trị là R nên 22x-1 có miền giá trị là 
do đó phương trình có nghiệm khi và chỉ khi –m2 + m > 0 hay 0 < m < 1.
CM
9 tháng 8 2019
Đáp án C.
Bất phương trình ⇔ log 2 5 x - 1 1 + log 2 5 x - 1 ≥ m
Đặt t = log 2 5 x - 1 , do x ≥ 1 ⇒ t ∈ [ 2 ; + ∞ )
Bất phương trình t 2 + t ≥ m ⇔ f ( t ) ≥ m
Với f ( t ) = t 2 + t , f ' ( t ) = 2 t + 1 > 0 với t ∈ [ 2 ; + ∞ ) nên hàm số f ( t ) đồng biến nên min ( t ) = f ( 2 ) = 6
Do đó theo bài ra để bất phương trình có nghiệm x ≥ 1 thì m ≤ min f ( t ) ⇔ m ≤ 6
Đáp án C
PT có nghiệm thực ⇔ m − 1 > 0 ⇔ m > 1