Trong không gian O x y z , cho mặt cầu S : x + 1 2 + y + 2 2 + z 2 = 4 và các điểm A − 2 ; 0 ; − 2 2 , B − 4 ; − 4 ; 0 . Biết rằng tập hợp các điểm M thuộc S và thỏa mãn M A 2 + M O → . M B → = 16 là một đường tròn. Tính bán kính đường tròn đó.
A. 3 2 4
B. 3 2
C. 3 7 4
D. 5 2










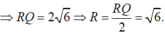




Đáp án C
⇒ x + 2 2 + y 2 + z + 2 2 2 + x x + 4 + y y + 4 + z 2 = 16
⇔ x 2 + y 2 + z 2 + 4 x + 2 y + 2 2 z − 2 = 0 S '
Giao tuyến của S và S ' là nghiệm của hệ phương trình:
S : x 2 + y 2 + z 2 + 2 x + 4 y + 1 = 0 , I − 1 ; − 2 ; 0 S ' : x 2 + y 2 + z 2 + 4 x + 2 y + 2 2 z − 2 = 0