Cho các mệnh đề:
1. Nếu hàm số y=f(x) liên tục trên và thì tồn tại sao cho
2. Nếu hàm số liên tục trên và thì phương trình có nghiệm.
3. Nếu hàm số y=f(x) liên tục, đơn điệu trên và thì phương trình có nghiệm duy nhất trên .
Trong ba mệnh đề trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng

Đáp án B
Nhìn đồ thị, ta thấy f' đổi dấu từ dương sang âm khi đi qua điểm x = -2, do đó x = -2 là điểm cực đại của hàm f => C đúng, B sai.
Tương tự, f’ đổi dấu từ âm sang dương khi đi qua điểm x = 0, do đó x = 0 là điểm cực tiểu của hàm f => A đúng.


Đáp án B
Quan sát đồ thị hàm số y = f ' x ta có:
f ' x > 0 ⇔ x < − 2 x > 0 , f ' x < 0 ⇔ − 2 < x < 0 ⇒ B sai; A,C và D đúng.

Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 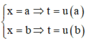
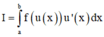


Chọn C.
Từ đồ thị dễ thấy hàm số nghịch biến và liên tục trên [-3;0] nên m a x [ - 3 ; 0 ] f ( x ) = f(-3)

Chọn C.
Từ đồ thị dễ thấy hàm số nghịch biến và liên tục trên [-3;0] nên
![]()
Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG