Tập hợp tất cả các số thực x thỏa mãn 2 3 4 x ≤ 3 2 2 - x là
A. - 2 3 ; + ∞ .
B. 5 2 ; + ∞ .
C. - ∞ ; 2 5 .
D. - ∞ ; 2 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
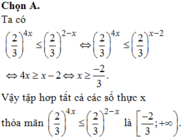
tách tách ra rồi mk làm cho, mk phụ bạn mấy câu thôi
C1: 17-|x-1|=15
|x-1|=17-15
|x-1|=2
nên x-1=2 hoặc x-1=-2
x=2+1 x=-2+1
x=3 x=-1
=>xE{-1;3}
C2: x-(-25-17-x)=6+x
x+25+17+x=6+x
x+x-x=6-25-17
x=-36
đánh sai đề rồi bạn êi, phải là \(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}=3\Leftrightarrow2x\sqrt{1-y^2}\) \(+2y\sqrt{2-z^2}+2z\sqrt{3-x^2}=6\)
<=> \(\left(x-\sqrt{1-y^2}\right)^2+\left(y-\sqrt{2-z^2}\right)^2+\left(z-\sqrt{3-x^2}\right)^2=0\)
<=> ..bla bla tự làm nhá !
Sử dụng Bất đẳng thức Bunyakovsky cho 2 bộ 3 số \(\left(\sqrt{1-y^2};\sqrt{2-z^2};\sqrt{3-x^2}\right)\) và \(\left(x,y,z\right)\) ta có
\(\left(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}\right)^2\le\left(x^2+y^2+z^2\right)\cdot\left[6-\left(x^2+y^2+z^2\right)\right]\left(1\right)\)
Đặt \(x^2+y^2+z^2=a\) ta có Bất đẳng thức (1) tương đương
\(9=\left(x\sqrt{1-y^2}+y\sqrt{2-z^2}+z\sqrt{3-x^2}\right)^2\le\left(a\right)\cdot\left(6-a\right)\)
\(=-a^2+6a-9+9=-\left(a-3\right)^2+9\le9\)
Dấu "=" xảy ra khi 
Giải hệ phương trình trên ta được 
Dấu "=" xảy ra khi \(\hept{\begin{cases}a=x^2+y^2+z^2=3\\\frac{x^2}{1-y^2}=\frac{y^2}{2-z^2}=\frac{z^2}{3-x^2}=1\end{cases}}\) giải hệ pt ta có \(\hept{\begin{cases}x=1\\y=0\\z=\sqrt{2}\end{cases}}\)
Thế nào nó bị lỗi nên không hiển thị