Cho hình chóp S . A B C D có đáy là hình vuông cạnh a . S A = a v à S A vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD
A. d = a 3 2
B. d = a 3 3
C. d = a 6 6
D. d = a 6 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Phương pháp:
Sử dụng lý thuyết d(a,b) = d(a,(P)) = d (M,(P)) với a, b là các đường thẳng chéo nhau, (P) là mặt phẳng chứa chứa b và song song với a, M là một điểm bất kì thuộc a.
Cách giải:
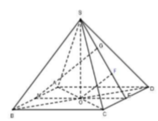
Gọi M, E là trung điểm của AB, CD và F, G là hinh chiếu của O, M lên SE.
Ta thấy:
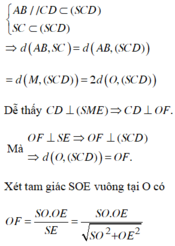
 nhân 2 rồi chọn ngay C là sai.
nhân 2 rồi chọn ngay C là sai.

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

Đáp án A
Gọi h là trung điểm của A B ⇒ S H ⊥ A B C D
Kẻ H K ⊥ S A K ∈ S A ⇒ H K ⊥ S A D ⇒ d H ; S A D = H K
Vì A D / / B C ⇒ B C / / m p S A D ⇒ d S A ; B C = d B C ; S A D
= d B ; S A D = 2 × d H ; S A D = 2 H K
Tam giác SAH vuông tại H, có H K = S H . H A S H 2 + H A 2 = a 3 4
Vậy d S A ; B C = 2 H K = 2. a 3 4 = a 3 2

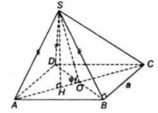
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
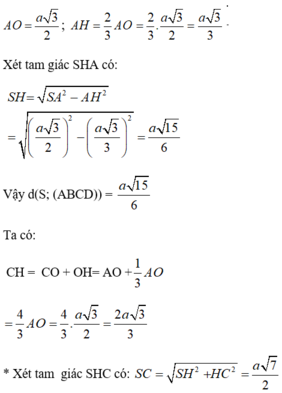


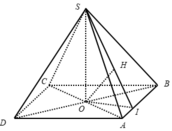
- Gọi O là giao điểm của AC và BD.
- Kẻ: OI ⊥ AB, OH ⊥ SI.
+) Ta có:
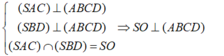
+) Ta lại có:
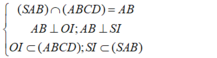
- Do đó, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng góc 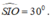
+) Khi đó: CD // AB nên CD // ( SAB).
Suy ra:

- Ta có:
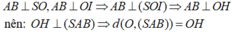
+) Tam giác ABC có BC = BA và 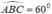 nên tam giác ABC đêù
nên tam giác ABC đêù
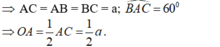
- Trong tam giác OIA có:
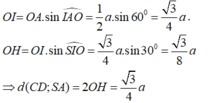
Đáp án D
Ta có: f ' x = x − 1 x 2 − 2 2 x 2 + 2 đổi dấu khi đi qua điểm x=1 nên hàm số đã cho có duy nhất 1 điểm cực trị.