trong mặt phẳng xOy cho điểm M(2;3). lập pt dường thẳng d đi qua M, sao cho khoảng cách từ o(0;0) đến đường thẳng d lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 10 2018
Chọn B.
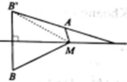
Dễ thấy A, B nằm khác phía so với mặt phẳng (xOy). Gọi B’ là điểm đối xừng với B qua (xOy). Thế thì B ' - 1 ; 4 ; 3 và M B = M B ' . Khi đó
Đẳng thức xảy ra khi và chỉ khi M, A, B’ thẳng hàng và M nằm ngoài đoạn AB’. Như vậy M cần tìm là giao điểm của đường thẳng AB’ và mặt phẳng (xOy). Đường thẳng AB có phương trình
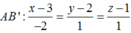
Từ đó tìm được M(5, 1, 0).
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 7 2021
\(\overrightarrow{MN}=\left(1;-3\right)\Rightarrow MN=\sqrt{10}\)
Đặt \(AB=a\)
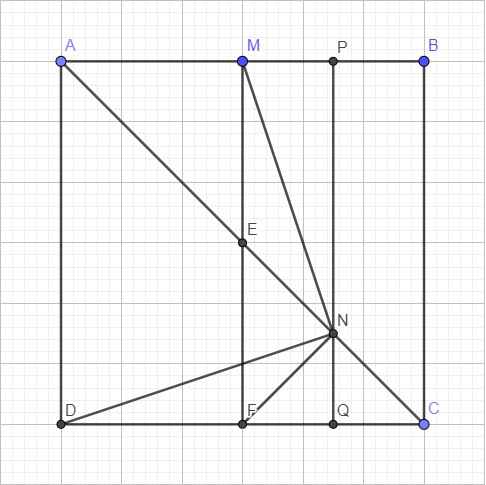
Qua N kẻ đường thẳng song song BC cắt AB và CD lần lượt tại P và Q, gọi F là trung điểm CD \(\Rightarrow MF\) song song và bằng BC
Theo Talet: \(\dfrac{PN}{BC}=\dfrac{AP}{AB}=\dfrac{AN}{AC}=\dfrac{3}{4}\Rightarrow PN=\dfrac{3a}{4}\) ; \(DQ=AP=\dfrac{3a}{4}\) ; \(MP=NQ=\dfrac{a}{4}\)
\(\Rightarrow MN^2=10=MP^2+PN^2=\dfrac{a^2}{16}+\dfrac{9a^2}{16}\Rightarrow a=4\)
\(\Rightarrow MF=4\) ; \(NQ=FQ=\dfrac{a}{4}\Rightarrow FN=\sqrt{NQ^2+FQ^2}=a\sqrt{2}\) ;
Đặt \(F\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MF}=\left(x-1;y-2\right)\\\overrightarrow{NF}=\left(x-2;y+1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+\left(y-2\right)^2=MF^2=16\\\left(x-2\right)^2+\left(y+1\right)^2=FN^2=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}F\left(1;-2\right)\\F\left(\dfrac{17}{5};-\dfrac{6}{5}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{MF}=\left(0;-4\right)=-4\left(0;1\right)\\\overrightarrow{MF}=\left(\dfrac{12}{5};-\dfrac{16}{5}\right)=\dfrac{4}{5}\left(3;-4\right)\end{matrix}\right.\)
Phương trình CD:
\(\left[{}\begin{matrix}0\left(x-1\right)+1\left(y+2\right)=0\\3\left(x-\dfrac{17}{5}\right)-4\left(y+\dfrac{6}{5}\right)=0\end{matrix}\right.\)
N
24 tháng 12 2017
\(\left\{{}\begin{matrix}\overrightarrow{MB}.\overrightarrow{MC}=0\\MB=MC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[\left(x_B-x\right)\overrightarrow{i}+\left(y_B-y\right)\overrightarrow{j}\right]\left[\left(x_c-x\right)\overrightarrow{i}+\left(y_C-y\right)\overrightarrow{j}\right]=0\\\sqrt{\left(x_B-x\right)^2+\left(y_B-y\right)^2}=\sqrt{\left(x_C-x\right)^2+\left(y_C-y\right)^2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(4-x\right)\left(-3-x\right)+\left(-2-y\right)\left(-1-y\right)=0\\\left(4-x\right)^2+\left(-2-y\right)^2=\left(-3-x\right)^2+\left(-1-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-x+3y-10=0\\y+5=7x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(x-1\right)=0\\y=7x-5\end{matrix}\right.\)
\(\Rightarrow\)M(x;y): (0;-5) ; (1;2)
CM
24 tháng 9 2018
Chọn B.
Dễ thấy các điểm A, B, C có tọa độ là A(-a, b, c), B(a, -b, c), C(a, b, -c). Thế thì tọa độ trọng tâm G của tam giác ABC sẽ là G a 3 ; b 3 ; c 3
d song song voi duong thang x=y thi khoảng cách từ o(0;0) đến đường thẳng d lớn nhất