Cho số phức z = 1 + i . Biết rằng tồn tại các số phức z 1 = a + 5 i , z 2 = b (trong đó a , b ∈ ℝ , b > 1 ) thỏa mãn 3 z − z 1 = 3 z − z 2 = z 1 − z 2 . Tính b − a
A. b − a = 5 3
B. b − a = 2 3
C. b − a = 4 3
D. b − a = 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Đặt ![]() lần lượt là các điểm biểu thị cho các số phức
z
,
z
1
,
z
2
lần lượt là các điểm biểu thị cho các số phức
z
,
z
1
,
z
2
Vậy ![]()
Từ giả thiết cho ta tam giác MNP cân tại M có ![]()


(nhân chéo vế với vế của hai phương trình).
Tìm được 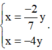 Thay vào (1) thì thấy chỉ có
Thay vào (1) thì thấy chỉ có  thỏa mãn. Lúc này do
thỏa mãn. Lúc này do ![]()
Do 
Vậy ![]()

Đáp án A
Gọi z = a + b i , khi đó z + 3 i = z + 2 − i
⇔ a 2 + b + 3 2 = a + 2 2 + b − 1 2
⇔ 4 a − 8 b = 4 ⇔ a = 1 + 2 b
Ta có: a 2 + b 2 = 1 + 2 b 2 + b 2 = 5 b 2 + 4 b + 1
= 5 b + 2 5 2 + 1 5 ≥ 1 5 ⇒ z . z ¯ = a 2 + b 2 = 1 5

Đáp án D.
Đặt z = a + bi => a + bi ![]()
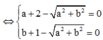
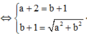
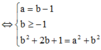

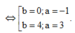
Do |z| > 1 => a = 3, b = 4
Đáp án D