Cho hàm số y = 2 cos 3 x - 3 cos 2 x - m cos x . Tìm tất cả các giá trị của m để hàm số đã cho nghịch biến trên khoảng 0 ; π 2
A. m ∈ [ - 3 2 ; + ∞ )
B. m ∈ - 2 ; 3 2
C. m ∈ 3 2 ; 2
D. m ∈ ( - ∞ ; - 3 2 ]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx
Hàm số nghịch biến trên R
![]()
Trường hợp 1: m= -1/ 2 ; ta có 0 ≤ 7 2 ∀ x ∈ ℝ
Vậy hàm số luôn nghịch biến trên R.
Trường hợp 2: m< -1/ 2 ; ta có
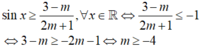
Trường hợp 3:m > -1/2 ; ta có:
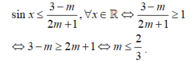
Vậy - 4 ≤ m ≤ 2 3

Chọn D.
Cách 1:
![]()
![]()
Hàm số y = 2 cos 3 x - 3 cos 2 x - m cos x nghịch biến trên khoảng 0 ; π 2
![]()

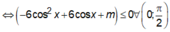
![]()
Xét 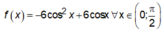
Đặt t = cosx
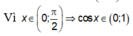
Ta có: ![]() là Parabol có đỉnh
là Parabol có đỉnh 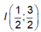 và hệ số a < 0 nên có giá trị lớn nhất là
3
2
tại t =
1
2
và hệ số a < 0 nên có giá trị lớn nhất là
3
2
tại t =
1
2
Để (1) xảy ra 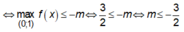
Cách 2:
Đặt t = cosx
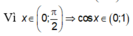
Ta có:
![]()
Hàm số y =
2
cos
3
x
-
3
cos
2
x
-
m
cos
x
nghịch biến trên khoảng
0
;
π
2
thì ![]() đồng biến trên khoảng (0;1)
đồng biến trên khoảng (0;1)
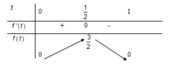
![]()
![]()
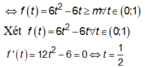
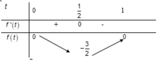
Dựa vào bảng biến thiên suy ra ![]()

Đáp án là C
Tập xác định : D = R \{m}
Ta có : y ' = 1 − m x − m 2
Hàm số nghịch biến trên khoảng (−¥;2) khi và chỉ khi y' <0, "x < 2, tức là : 1 − m < 0 m ≥ 2 ⇔ m ≥ 2 . Vậy tập giá trị m cần tìm là [2; + ∞ )

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)
Đáp án là D