Nêu ví dụ về nhị thức Newton
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KA
1
CT
10 tháng 11 2021
Tham khảo :
Nhị thức Newton là 1 công thức khai triển hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n ((a+b)n) thành một đa thức có n+1 số hạng.
HT
Công thức
NN
3
NN
24 tháng 11 2016
Người lớn đang nói chuyện thì không xen vào
Ho che miệng lại
...
7 tháng 12 2016
Lịch sự tế nhị:
+ Không được nói leo
+ Nói năng lịch sự, đàng hoàng ko dc nói cộc lốc
+ Kính trên nhường dưới
+ Không được tò mò chuyện của người khác
NK
6
NN
5 tháng 11 2016
Bạn có thể tham khảo sách giáo dục công dân lớp 6 bài Lịch sự , tế nhị
Chúc bạn học tốt ! 
5 tháng 11 2016
- Đến nhà người khác phải khách sáo, không quá thoải mái như nhà mình.
LN
Có ai có thể cho mình các ví dụ về đa thức DƯỚI dạng tổng bình Phương một nhị thức với một hằng số ?
0
17 tháng 12 2016
lịch sự , tế nhị là Những cử chỉ , hành vi dùng trong giao tiếp , ứng sử phù hợp với quy định của xã hội , thể hiện truyền thống đạo đức của nhân dân , dân tộc . VD : Hiền phải đi học về bằng xe buýt .Xe vừa tới nơi hiền tìm chỗ ngồi . Đến trạm tiếp theo , lúc lên xe Hiền thấy 1 người phụ nữ tay xách đồ, tay bế con cứ loay hoay tìm chỗ ngồi . Thấy thế Hiền bảo người phụ nữ , " Cô ơi , cô bế em vào ngồi chỗ này đi ạ ! " Người phụ nữ nhìn Hiền trìu mến nói : " Cô cảm ơn cháu " . Hiền thấy trong lòng mình rất vui 
25 tháng 8 2019
Chuỗi 1: Kiến ăn cỏ, ếch ăn kiến, rắn ăn ếch, ếch chết xác phân hủy để cỏ hấp thụ.
Chuỗi 2: Châu chấu ăn cỏ, chuột ăn châu chấu, rắn ăn chuột, diều hâu ăn rắn rồi thải phân làm chất bón cho cỏ.
21 tháng 12 2021
Tham khảo
Nhị thức Newton là 1 công thức khai triển hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n thành một đa thức có n+1 số hạng.
21 tháng 12 2021
Tham khảo:
Trong toán học, định lý khai triển nhị thức là một định lý toán học về việc khai triển hàm mũ của tổng. Cụ thể, kết quả của định lý này là việc khai triển một nhị thức bậc n thành một đa thức có {\displaystyle n+1} số hạng: {\displaystyle ^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}a^{k}}
TP
24 tháng 11 2021
Tham khảo
Trong toán học, định lý khai triển nhị thức (ngắn gọn là định lý nhị thức) là một định lý toán học về việc khai triển hàm mũ của tổng. Cụ thể, kết quả của định lý này là việc khai triển một nhị thức bậc {\displaystyle n} thành một đa thức có {\displaystyle n+1} số hạng:
thành một đa thức có {\displaystyle n+1}
số hạng:{\displaystyle (x+a)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}a^{k}}
với:
{\displaystyle {n \choose k}={\frac {n!}{(n-k)!k!}}}
Gọi là số tổ hợp chập k của n phần tử.
Định lý này đã được độc lập chứng minh bởi hai người đó là:
Nhà toán học và cơ học Isaac Newton tìm ra trong năm 1665.Nhà toán học James Gregory tìm ra trong năm 1670.Công thức đã giới thiệu còn mang tên là Nhị thức Newton.
12 tháng 10 2018
5= 101
6=10
9=101
12=100
( bạn cứ chia cho 2 rồi lấy số dư rồi viết ngược từ số dư cuối lên trên )
đáp án trên mình nghĩ vậy. k nha!! mình đang âm điểm
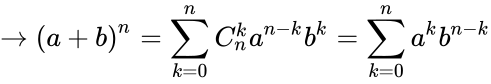
Tham khảo :
chrome-untrusted://new-tab-page/custom_background_image?url=https%3A%2F%2Flh5.googleusercontent.com%2Fproxy%2FtjJRG8ELyrHCJQ18ThdF1ybYJ9CP1q6jDyCAECruLxqefc2gvH9YYUjKItQyvmWClmOoC3XivqciC7PbY2-
1NtWxLE7fNsJFqYflxTi2EyE%3Dw3840-h2160-p-k-no-nd-mv