Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và FChứng minh rằng OE = OF.

DH

Đào Hải Ngọc

31 tháng 1 2016 - olm

Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và F

Chứng minh rằng OE = OF.

#Toán lớp 8

1

ZR

Zoro Roronoa

31 tháng 1 2016

Tam giác ABD có OE//AB

=>DO/DB = OE/AB (Theo hệ quả Đlý Ta-lét) (1)
Tam giác ABC có OF//AB

=>CO/CA = OF/AB (Theo hệ quả Đlý Ta-lét) (2)
Tam giác ABO có CD//AB

=>OD/OB = OC/OA (Theo hệ quả Đlý Ta-lét)
=> OD/(OB+OD) = OC/(OA+OC) hay OD/DB=CO/CA (3)
Từ (1) (2) và (3)

=> OE/AB = OF/AB
=> OE = OF (đpcm.)

Đúng(0)

KH

Kamato Heiji

8 tháng 3 2021

1. Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F . Chứng minh rằng OE = OF

#Toán lớp 8

1

HQ

Huỳnh Quang Sang

14 tháng 3 2021

Bạn tự vẽ hình nhé

Xét $\Delta ACD$ có OE // CD(gt)

=> $\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)$

Xét $\Delta BCD$ có OF // CD (gt)

=> $\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)$

Mặt khác AB // CD nên $\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)$

Từ $\left(1\right),\left(2\right),\left(3\right)$

=> $\dfrac{OE}{DC}=\dfrac{OF}{DC}$ => OE = OF

Đúng(1)

PT

Pham Trong Bach

12 tháng 8 2019

Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).

Chứng minh rằng OE = OF

#Toán lớp 8

1

CM

Cao Minh Tâm

12 tháng 8 2019

Giải bài 20 trang 68 SGK Toán 8 Tập 2 | Giải toán lớp 8

Đúng(2)

G

Gallavich

17 tháng 3 2021

1.Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F . Chứng minh rằng OE = OF 2.a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác trong AD. Tính diện tích tam giác ADM, biết AB = m, AC = n (n m) và diện tích tam giác ABC là S. b) Khi cho n = 7cm, m = 3cm, hỏi rằng diện tích tam giác...

Đọc tiếp

#Toán lớp 8

5

AH

Akai Haruma

Giáo viên

17 tháng 3 2021

Bài 1:

Áp dụng định lý Talet cho $EO\parallel DC$:

$\frac{OE}{DC}=\frac{AO}{AC}(1)$

Áp dụng định lý Talet cho $OF\parallel DC$:

$\frac{OF}{DC}=\frac{OB}{BD}(2)$

Áp dụng định lý Talet cho $AB\parallel CD$:

$\frac{OA}{OC}=\frac{OB}{OD}\Leftrightarrow \frac{OA}{OA+OC}=\frac{OB}{OB+OD}\Leftrightarrow \frac{OA}{AC}=\frac{OB}{BD}(3)$

Từ $(1);(2);(3)\Rightarrow \frac{OE}{DC}=\frac{OF}{DC}$

$\Rightarrow OE=OF$ (đpcm)

Đúng(3)

AH

Akai Haruma

Giáo viên

17 tháng 3 2021

Hình bài 1:

undefined

Đúng(2)

KH

Kamato Heiji

21 tháng 4 2020

1. Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F . Chứng minh rằng OE = OF2.a) Cho tam giác ABC với đường trung tuyến AM và đ...

#Toán lớp 8

0

KH

Kamato Heiji

21 tháng 4 2020

M làm cái j đấy

Đúng(0)

HV

Hạ Vy

21 tháng 4 2020

Hàn Thất haizz

Chủ tịch giả nghèo… và cái kết: 'Đừng coi thường người khác vì vẻ ...

Đúng(0)

NM

Nguyễn Mai Thu

22 tháng 3 2023

Cho hình thang ABCD (AB//CD). Hai đường chéo AC và BDcắt nhau tại O . đường thẳng A đi qua O và song song với đáy của hình thang cách các cạnh bên AD,BC theo thứ tự tại E và F chứng minh rằng OE=OF

#Toán lớp 8

1

DT

Đinh Trí Gia BInhf

22 tháng 3 2023

Xét tam giác ADC có EO // CD nên :

$\frac{O E}{C D} = \frac{A O}{A C} (1)$ (Hệ quả định lí ta- let).

Xét tam giác BDC có OF // CD nên:

$\frac{O F}{C D} = \frac{B F}{B C} (2)$ ( hệ quả định lí Ta- let)

Xét tam giác ABC có OF // AB nên theo định lí Ta – let :

$\frac{A O}{A C} = \frac{B F}{B C} (3)$

Từ (1); (2); (3) suy ra:

$ \frac{O E}{C D} = \frac{A O}{A C} = \frac{B F}{B C} = \frac{O F}{C D}$

$\Rightarrow O E = O F$ (đpcm)

Đúng(3)

NM

Nguyễn Mai Thu

22 tháng 3 2023

thanhkiu

Đúng(0)

SG

Sách Giáo Khoa

22 tháng 4 2017

Cho hình thang ABCD (AB//CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh bên AD, BC theo thứ tự tại E và F (h.26)

Chứng minh rằng OE = OF

#Toán lớp 8

2

TN

Tuyết Nhi Melody

22 tháng 4 2017

Giải:

∆ADC có OE // OC nên

$\frac{O E}{D C}$ = $\frac{A E}{A D}$

∆BDC có OF // DC nên $\frac{O F}{D C}$ = $\frac{B F}{B C}$

Mà AB // CD => $\frac{A E}{A D}$ = $\frac{B F}{B C}$ (câu b bài 19)

Vậy $\frac{O E}{D C}$ = $\frac{O F}{D C}$ nên OE = OF.

Đúng(0)

LN

Lê Nhật Phương

16 tháng 1 2018

:

Giải bài 20 trang 68 SGK Toán 8 Tập 2 | Giải toán lớp 8

Đúng(0)

EL

Emily Linh

11 tháng 1 2016 - olm

Cho hình thang ABCD ( AB//CD) , các đường chéo cắt nhau tại O . Qua O kẻ đường thẳng song song với hai đáy , cắt các cạnh bên AC và BC theo thứ tự tại E và F .

Chứng minh rằng OE = OF

#Toán lớp 9

2

ML

Minh Lê Thái Bình

11 tháng 1 2016

SAi đề r bạn ơi cạnh bên AD chứ

Đúng(0)

ML

Minh Lê Thái Bình

11 tháng 1 2016

Vì OE // DC ==> OA/AC = OE/DC (định lý Ta-let) (1)
Vì OF // DC ==> OB/BD = OF/DC (định lý Ta-let) (2)
Vì AB // CD ==> OA/OC = OB/OD (định lý ta-let)
Theo tính chất dãy tỉ số bằng nhau ta có:
OA/OC = OB/OD <=> OA / (OA + OC) = OB / (OB + OD)
<=> OA / AC = OB / BD (3)
Từ (1), (2) và (3) suy ra ta có:
OE / DC = OF / DC <=> OE = OF (đpcm)

Đúng(0)

PT

Pham Trong Bach

5 tháng 12 2017

Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.

#Toán lớp 8

1

CM

Cao Minh Tâm

5 tháng 12 2017

Trong ΔDAB, ta có: OM // AB (gt)

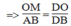Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8 (Hệ quả định lí Ta-lét) (1)

Trong ΔCAB, ta có: ON // AB (gt)

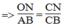Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8 (Hệ quả định lí Ta-lét) (2)

Trong ΔBCD, ta có: ON // CD (gt)

Suy ra: (định lí Ta-lét) (3)

Từ (1), (2) và (3) suy ra: 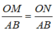Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Vậy: OM = ON

Đúng(0)

TH

ta huy hoang

21 tháng 6 2015 - olm

Cho hình thang ABCD(AB//CD).Hai đường chéo AB và CD cắt nhau tại O và song song với đáy của hình thang.Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh bên AD,BCtheo thứ tự tại E và F.Chứng minh rằng OE=OF.

Giúp mình làm bài này nhé!

Và kẻ giúp mình cái hình nữa nhé!

#Toán lớp 8

3

TN

Trinh Nguyễn Thị

3 tháng 7 2016

k có ai tl cau này à

Đúng(0)

CH

Cô Hoàng Huyền

Admin VIP

26 tháng 2 2018

Câu hỏi của trần trúc quỳnh - Toán lớp 9 - Học toán với OnlineMath

Em tham khảo tại ý a của bài này nhé.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP