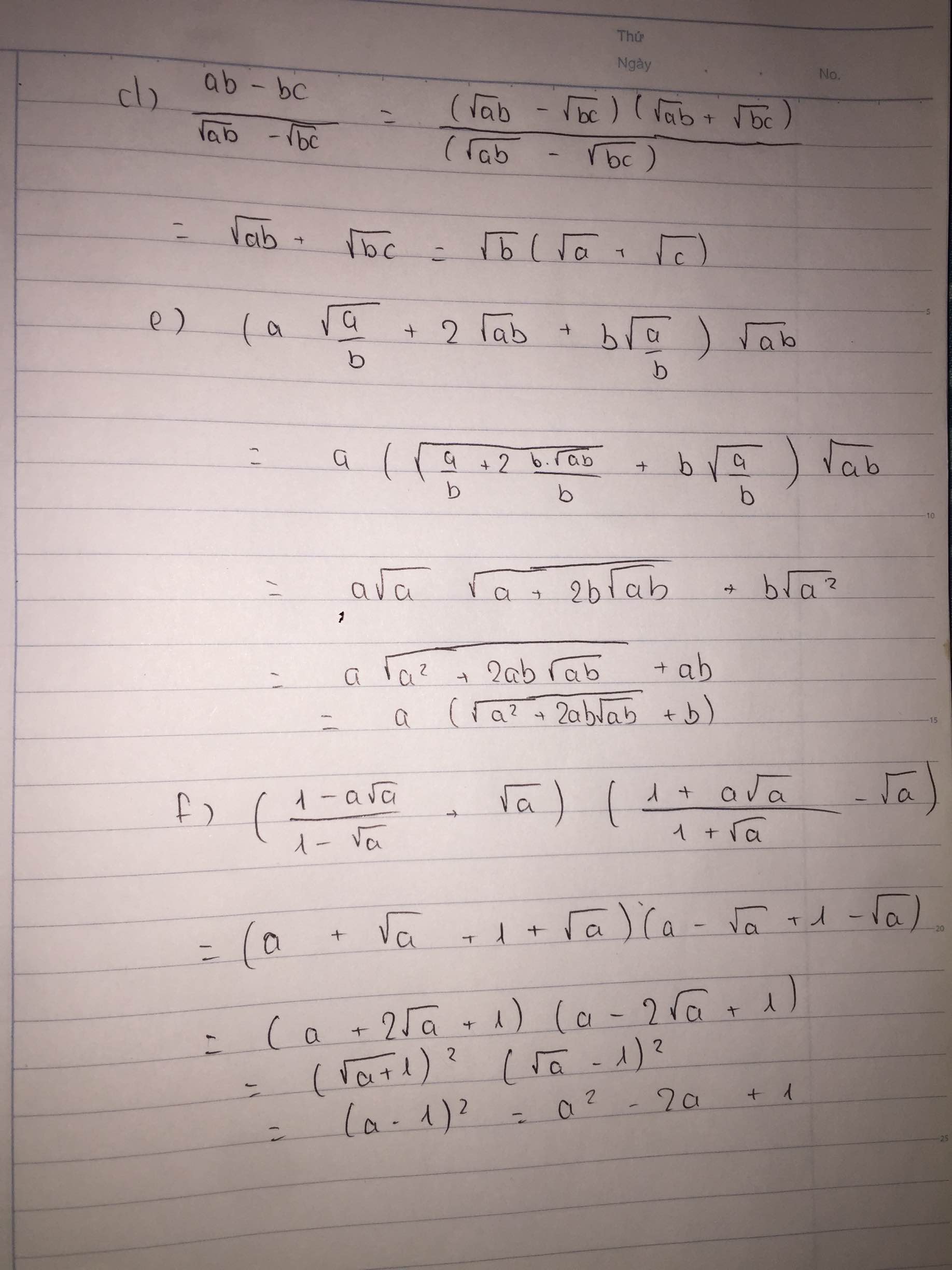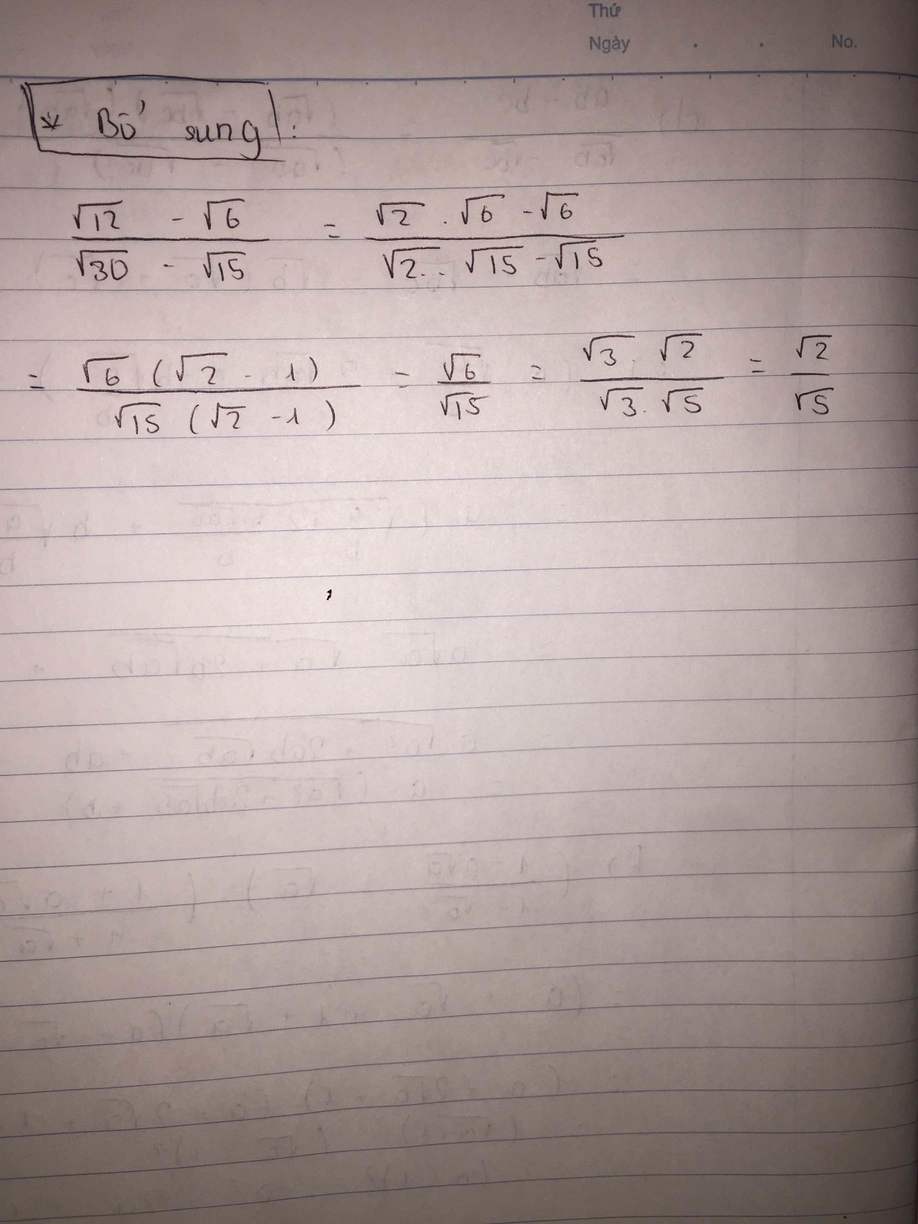Cho m hỏi câu e và f với ạ. M cảm ơn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
2
28 tháng 4 2017
A B C I H F K M N
a) Câu này bạn làm được rồi nhưng mình vẫn nói qua:
Tam giác ABK=Tam giác IBK (Cạnh huyền góc nhọn)
b) Từ điểm I vẽ đường thẳng vuông góc với AC, cắt AC tại điểm N.
Ta có: IN vuông góc với AC, AB vuông góc với AC tại A
=> IN//AB (Quan hệ song song vuông góc)
=>^BAI=^NIA (So le trong) (1)
Lại có: Tam giác ABK= Tam giác IBK (Bạn đă c/m đc)=> AB=IB (2 cạnh tương ứng)
=> Tam giác ABI cân tại đỉnh B=> ^BAI=^BIA (hay ^BAI=^HIA) (2 góc ở đáy) (2)
Từ (1) và (2)=> ^HIA=^NIA.
Xét tam giác HAI và tam giác NAI:
^AHI=^ANI=90o
AI chung => Tam giác HAI=Tam giác NAI (Cạnh huyền góc nhọn)
^HIA=^NIA
=> ^HAI=^NAI (2 góc tương ứng)=> AI là phân giác của ^HAN hay AI là phân giác của ^HAC (đpcm)
c)+) AH vuông góc với BC, F thuộc AH; IK cũng vuông góc với BC=> AF song song với IK (Quan hệ song song vuông góc)
=> ^AFK=^IKF (So le trong) (3)
Ta có: Tam giác ABK = Tam giác IBK (Đã cm ở câu a) (Câu a rất quan trọng)
=> ^AKB=^IKB. Mà F cũng thuộc BK=> ^AKF=^IKF (4)
Từ (3) và (4)=> ^AFK=^AKF=> Tam giác AFK cân tại A theo tính chất 2 góc ở đáy của tam giác cân (đpcm)
+) Ta có: AH vuông góc với BC, BC là đường xiên => AH<AC (Quan hệ đường xiên hình chiếu) (5)
Mà F thuộc AH=> AF<AH (6)
Từ (5) và (6)=> AF<AC (đpcm)
d) AM=AC=> AF+FM=AK+KC (7)
Mà tam giác AFK cân tại A=> AF=AK (8)
Từ (7) và (8)=> FM=KC.
AI là phân giác của ^HAC=> AI cũng là phân giác của ^MẠC=> ^MAI=^CAI
Xét tam giác AIM và tam giác AIC:
AI chung
^MAI=^CAI => Tam giác AIM= Tam giác AIC (c.g.c)
AM=AC
=> IM=IC (2 cạnh tương ứng) và ^AMI=^ACI (2 góc tương ứng) (hay ^FMI=^KCI)
Xét tam giác FIM và tam giác KIC:
FM=KC
^FMI=^KCI => Tam giác FIM= Tam giác KIC (c.g.c)
IM=IC
=> ^FIM=^KIC (2 góc tương ứng). Mà KI vuông góc với BC => ^KIC=90o
=> ^FIM=90o => IM vuông góc với IF (đpcm).
HK
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
2
5 tháng 2 2022
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
26 tháng 9 2023
\(A\cap B\\ \Leftrightarrow\left\{{}\begin{matrix}m+2< 0\\m+1< 1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m< 0\end{matrix}\right.\\ hay.m\in\left[-\infty;-1\right]\cap\left[1;+\infty\right]\)
HT
0
