Cho biết U 92 238 và U 92 235 là các chất phóng xạ có chu kì bán rã lần lượt là T 1 = 4,5. 10 9 năm và T2 = 7,13. 10 8 năm. Hiện nay trong quặng urani thiên nhiên có lẫn U 238 và U 235 theo tỉ lệ 160 : 1. Giả thiết ở thời điểm tạo thành Trái Đất tỉ lệ 1: 1. Cho ln10 = 2,3 và ln2 = 0,693. Tuổi của Trái Đất là
A. 6,2 tỉ năm
B. 5 tỉ năm.
C. 5,7 tỉ năm.
D. 6,5 tỉ năm.

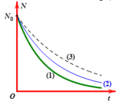
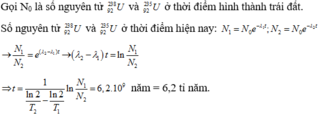
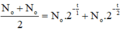
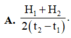
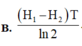
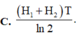
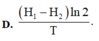

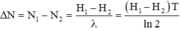
Chọn A