Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng a 3 2 6 . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC)
A. a 6 3 .
B. a 6 3 .
C. a 6 6 .
D. a 6 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 4 2018
Đáp án B
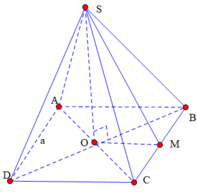
Gọi M là trung điểm BC; Gọi d là khoảng cách từ A tới (SBC)
Ta có:
CM
2 tháng 8 2019
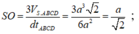
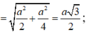
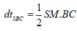
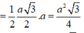
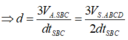
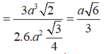
Đáp án là C.
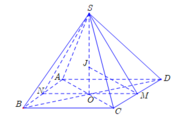
Gọi O là tâm hình vuông ABCD .Ta có đường cao của hình chóp SABCD là SO
V S A B C D = 1 3 S 0 . S A B C D ⇔ 3 6 a 8 = 1 3 S O . a 2 ⇒ S O = 3 2 a .
Xét tam giác SMO ta có SM= S 0 2 + O M 2 = ( 3 2 a ) 2 + ( a 2 ) 2 = a
Gọi M,N lần lượt là trung điểm của AB,CD.Khi đó J là tâm đường tròn nội tiếp tam giác SMN. Khi đó ta có MJ là đường phân giác của tam giác SMN.
Suy ra : S J J O = M S M O = a a = 2 ⇒ S J = 2 J O .
Mà S 0 = S J + J O = 3 2 a ⇔ 3 J O = 3 2 a ⇔ J O = 3 6
CM
1 tháng 7 2017
Chọn D.
Gọi H, M, N theo thứ tự là các trung điểm của các cạnh AC, BC, AD.
Kẻ NI ⊥ SM (I ∈ SM). Để ý rằng AN // (SBC)
Do đó NI = d(N,(SBC)) = d(A,(SBC)) = a 6 3
Từ hai tam giác đồng dạng SHM và NIM ta tính được SH.
Đáp án B.
Gọi M là trung điểm BC ; Gọi d là khoảng cách từ A tới (SBC)
S O = 3 V S . A B C D d t A B C D = 3 a 3 2 6 a 2 = a 2
S M = S O 2 + M O 2 = a 2 2 + a 2 4 = a 3 2
d t S B C = 1 2 S M . B C = 1 2 a 3 2 . a = a 2 3 4
⇒ d = 3 V A . S B C d t S B C = 3 V S . A B C D 2 d t S B C = 3 a 3 2 2.6. a 2 3 4 = a 6 3