Cho ba điểm Lập phương trình mặt phẳng (MNP) , biết điểm P là hình chiếu vuông góc của điểm A lên trục Ox
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.

Do các đường thẳng đôi một cắt nhau tại các điểm A, B, C nên các điểm cách đều các cạnh gồm tâm đường tròn nội tiếp và ba tâm đường tròn bàng tiếp.
Vậy có tất cả 4 điểm M cách đều ba đường thẳng đã cho.
đáp án D

ĐÁP ÁN B
Do d1 song song với d3 nên những điểm cách đều chúng nằm trên đường thẳng ∆ song song cách đều d1;d3.
Gọi khoảng cách hai đường thẳng d1, d3 là a > 0.
Khoảng cách giữa 2 đường thẳng ∆ và d1; ∆ và d3 là a/2
Trên đường thẳng ∆ có hai điểm A, B thỏa mãn d A , d 2 = d B , d 2 = a 2
Khi đó, hai điểm A, B là hai điểm cần tìm
Số điểm M cách đề ba đường thẳng là 2.

M thuộc Oy \(\Rightarrow M\left(0;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;1\right)\\\overrightarrow{BM}=\left(1;y-3\right)\end{matrix}\right.\)
ABM vuông tại B \(\Rightarrow\overrightarrow{AB}.\overrightarrow{BM}=0\)
\(\Rightarrow-2+y-3=0\Rightarrow y=5\)
\(\Rightarrow M\left(0;5\right)\)

Chọn B
Đặt M(x;y;z). Lập hệ 3 phương trình ba ẩn x,y,z từ phương trình mặt phẳng (P) và điều kiện MA=MB, MA=MC

Đáp án D
Do M thuộc d nên M( x; 2x+ 3)
Suy ra:
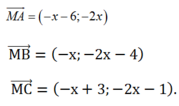
Do đó:
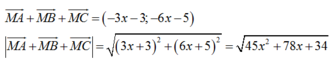
nhỏ nhất khi và chỉ khi: f(x) = 45x2+ 78x + 34 nhỏ nhất
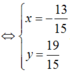



Đáp án D