Tính đạo hàm cấp 2018 của hàm số y = e 2 x .
A. y 2018 = 2 2017 . e 2 x .
B. y 2018 = 2 2018 . e 2 x .
C. y 2018 = e 2 x .
D. y 2018 = 2 2018 . x e 2 x .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có: y ' = 2 e 2 x ; y 2 = 2 2 . e 2 x ⇒ y 2018 = 2 2018 e 2 x .

Ta có:
![]()
Từ BXD của f ' ' x ta suy ra BBT của f ' x như sau:
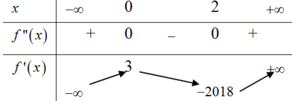
Từ BBT ta có:
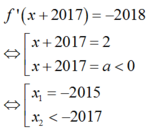
Từ đó ta suy ra BBT của hàm số f ' x + 2017 + 2018 như sau:
Tịnh tiến đồ thị hàm số y = f ' x lên trên 2018 đơn vị.
Tịnh tiến đồ thị hàm số y = f ' x sang trái 2017 đơn vị.
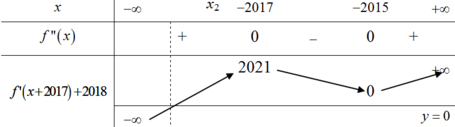
Suy ra BBT của hàm số y = f ' x + 2017 + 2018 x

Vậy hàm số đạt GTNN tại x 2 < - 2017
Chọn B.

\(a,y'=8x^3-10x\\ \Rightarrow y''=24x^2-10\\ b,y'=e^x+xe^x\\ \Rightarrow y''=e^x+e^x+xe^x=2e^x+xe^x\)

Đáp án C
Vì phương trình ![]() có ba nghiệm phân biệt nên đồ thị hàm số
có ba nghiệm phân biệt nên đồ thị hàm số 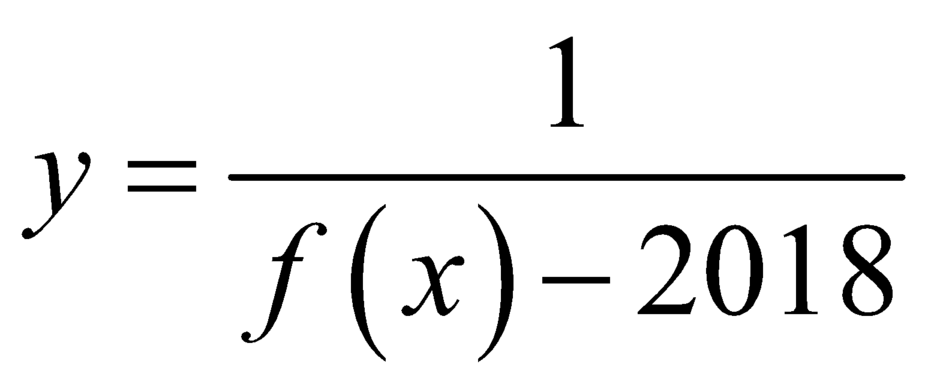 có ba đường tiệm cận đứng.
có ba đường tiệm cận đứng.
Mặt khác, ta có:
![]()
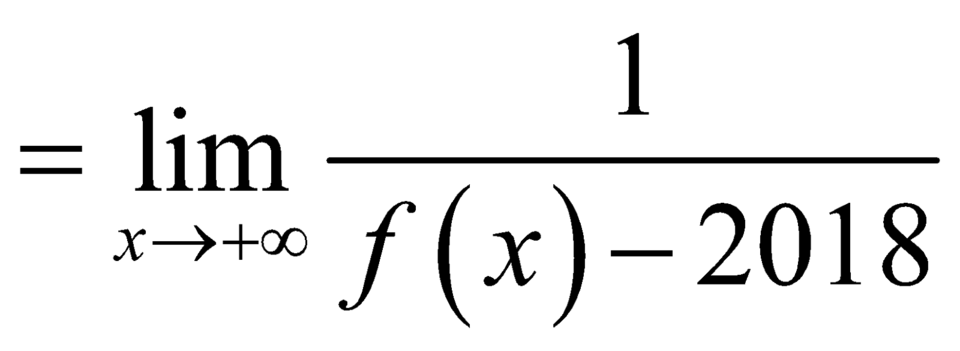
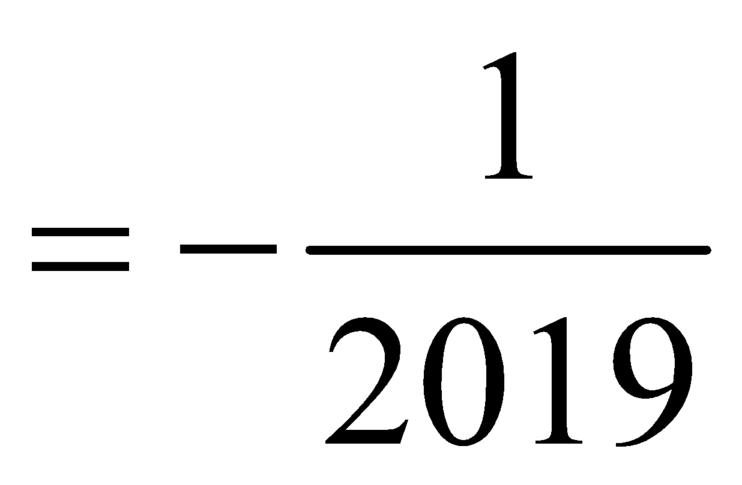 nên đường thẳng
nên đường thẳng ![]() là đường tiệm cận ngang của đồ thị hàm số
là đường tiệm cận ngang của đồ thị hàm số 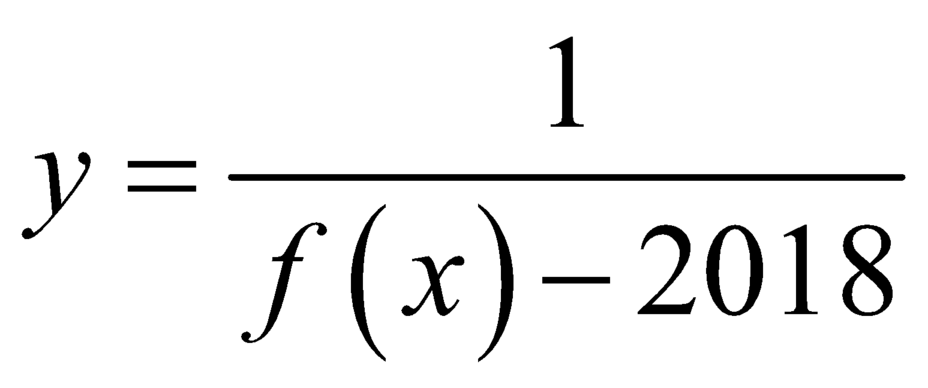 .
.
Và ![]()
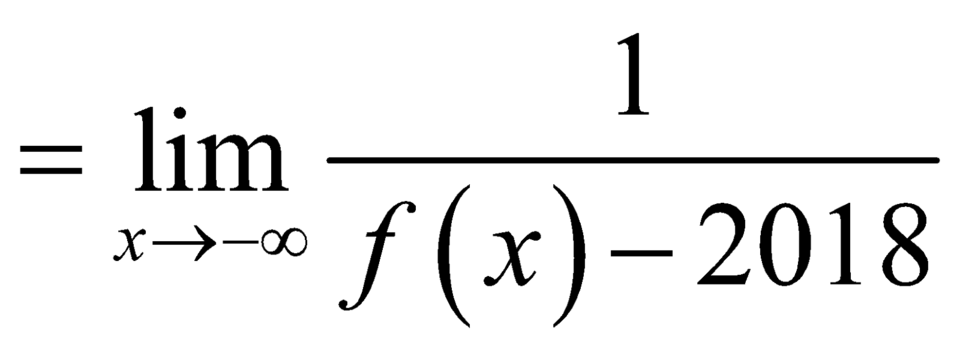
![]() nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số
nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số 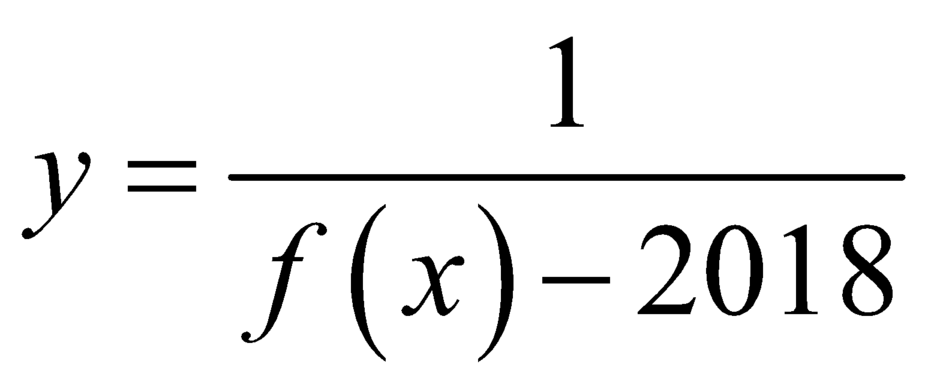 .
.
Vậy ![]() .
.

\(a,y'=3x^2-4x+2\\ \Rightarrow y''=6x-4\\ b,y'=2xe^x+x^2e^x\\ \Rightarrow y''=4xe^x+x^2e^x+2e^x\)
Đáp án A
Ta có y ' = 2 e 2 x ; y ' ' = 2 2 e 2 x ; ... ; y 2018 = 2 2018 e 2 x