Trong không gian Oxyz, cho điểm M 2017 ; 2018 ; 2019 . Hình chiếu vuông góc của điểm M trên trục Oz có tọa độ là:
A. 2017 ; 0 ; 0
B. 0 ; 0 ; 2019
C. 0 ; 2018 ; 0
D. 0 ; 0 ; 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp:
lần lượt là các VTPT. Khi đó, góc giữa hai mặt phẳng α , β được tính
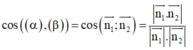
Cách giải:
(P): x+2y-2z+2018=0
(Q): x+my+(m-1)z+2017=0
Góc giữa hai mặt phẳng (P) và (Q):
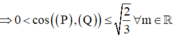
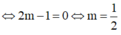
Khi đó
Ta thấy:
Đáp án A
Phương pháp:
Cho 
; 
nhận
n
1
→
=
a
1
;
b
1
;
c
1
;
n
2
→
=
a
2
;
b
2
;
c
2
lần lượt là các VTPT. Khi đó, góc giữa hai mặt phẳng
α ; β được tính: cos α ; β = cos n 1 → ; n 2 → = n 1 → . n 2 → n 1 → n 2 →
Với 0 0 ≤ α ≤ 90 0 ⇒ α m i n ⇔ cos α m a x
Cách giải:
(P): x + 2y – 2z +2018 = 0 có 1 VTPT: n 1 → = 1 ; 2 ; - 2
(Q): x + my + (m – 1)z + 2017 = 0 có 1 VTPT: n 2 → = 1 ; m ; m - 1
Góc giữa hai mặt phẳng (P) và (Q):
cos P ; Q = cos n 1 → ; n 2 → = n 1 → . n 2 → n 1 → n 2 →
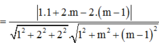
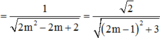
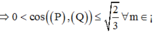
Với 0 0 ≤ α ≤ 90 0 ⇒ α m i n ⇔ cos α m a x
=>((P),(Q))min khi và chỉ khi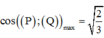 
Khi đó,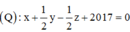 
Ta thấy: 
Đáp án D
Phương pháp: (Oxy): z = 0, (Oyz): x = 0, (Oxz): y = 0
Trục Oy: x = 0 y = t z = 0
Cách giải: M (1;0;3) ∈ (Oxz)
Chọn B
Gọi A (0;0;a). Đường thẳng AB qua A và vuông góc với (α) có phương trình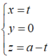 
B là hình chiếu của A lên (α) nên tọa độ B thỏa mãn hệ
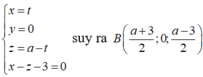
Tam giác MAB cân tại M nên
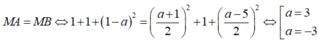
·Nếu a=-3 thì tọa độ A (0;0;-3) và B (0;0;-3) trùng nhau, loại.
·Nếu a=3 thì tọa độ A (0;0;3), B (3;0;0).
Diện tích tam giác MAB bằng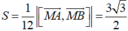 
Đáp ánC
Phương pháp: Điểm M(a;b;c) có hình chiếu trên trục Ox, Oy, Oz lần lượt là:
Cách giải: Hình chiếu của M lên trục Oy là Q(0;2;0)
Chọn A
Vectơ pháp tuyến của (P) và (Q) lần lượt là
Gọi φ là góc tạo bởi hai mặt phẳng (P) và (Q) thì 00 ≤ φ ≤ 900
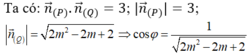
Để (P) và (Q) tạo với nhau một góc nhỏ nhất thì cosφ lớn nhất 
nhỏ nhất.
Mà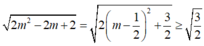 
nên giá trị lớn nhất của là 
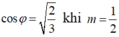khi m = 1/2
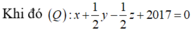
Vậy H (-2017; 1; 1) ∈ (Q)
Hình chiếu vuông góc của điểm M 2017 ; 2018 ; 2019 trên trục Oz có tọa độ là: M ' 0 ; 0 ; 2019 .
Chọn: B