Gọi M(x;y) là các điểm biểu diễn cho số phức z thỏa mãn Khi đó thỏa mãn hệ thức nào dưới đây?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
M ( x ) = P ( x ) − Q ( x ) = − 6 x 5 − 4 x 4 + 3 x 2 − 2 x − 2 x 5 − 4 x 4 − 2 x 3 + 2 x 2 − x − 3 = − 8 x 5 + 2 x 3 + x 2 − x + 3 Có M ( − 1 ) = − 8. ( − 1 ) 5 + 2 ⋅ ( − 1 ) 3 + ( − 1 ) 2 − ( − 1 ) + 3 = 11
Chọn đáp án A

Chọn A.
ĐK: 1 ≤ x ≤ 7
Ta có ![]()
Xét y(1) = y(7) = 6 , y(4) = 2 3 suy ra 2,44 < k < 3,464 suy ra k = 3 có 1 số nguyên k.

Bài 2:
\(41-2^x-1=9\)
\(\Rightarrow40-2^x=9\)
\(\Rightarrow2^x=31\)
\(\Rightarrow x\in\left\{\varnothing\right\}\)
Vậy không có giá trị x thỏa mãn
b) \(\left|x-3\right|-21=-5\)
\(\Rightarrow\left|x-3\right|=16\)
\(\Rightarrow x-3=\pm16\)
+) \(x-3=16\Rightarrow x=19\)
+) \(x-3=-16\Rightarrow x=-13\)
Vậy \(x\in\left\{19;-13\right\}\)
d) Ta có: \(M=7+7^2+...+7^{2016}\)
\(\Rightarrow7M=7^2+7^3+...+7^{2017}\)
\(\Rightarrow7M-M=\left(7^2+7^3+...+7^{2017}\right)-\left(7+7^2+...+7^{2016}\right)\)
\(\Rightarrow6M=7^{2017}-7\)
\(6M+7=7^{x+1}\)
\(\Rightarrow7^{2017}-7+7=7^{x-1}\)
\(\Rightarrow7^{x-1}=7^{2017}\)
\(\Rightarrow x-1=2017\)
\(\Rightarrow x=2018\)
Vậy \(x=2018\)
g) Ta có: \(x+9⋮x-2\)
\(\Rightarrow\left(x-2\right)+11⋮x-2\)
\(\Rightarrow11⋮x-2\)
\(\Rightarrow x-2\in\left\{1;-1;11;-11\right\}\)
+) \(x-2=1\Rightarrow x=3\)
+) \(x-2=-1\Rightarrow x=1\)
+) \(x-2=11\Rightarrow x=13\)
+) \(x-2=-11\Rightarrow x=-9\)
Vậy \(x\in\left\{3;1;13;-9\right\}\)
Bài 3:
a) \(\left(x+1\right)^{100}+\left|y-3\right|=0\)
\(\Rightarrow\left(x+1\right)^{100}=0\) và \(\left|y-3\right|=0\)
+) \(\left(x+1\right)^{100}=0\Rightarrow x+1=0\Rightarrow x=-1\)
+) \(\left|y-3\right|=0\Rightarrow y-3=0\Rightarrow y=3\)
Vậy \(x=-1;y=3\)

\(\Delta=\left(2m+3\right)^2-4m=4m^2+12m+9-4m=4m^2+8m+9\)
\(=4\left(m^2+2m+1-1\right)+9=4\left(m+1\right)^2+5\ge5>0\forall m\)
Vậy pt luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=2m+3\\x_1x_2=m\end{matrix}\right.\)Ta có : \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(\left(2m+3\right)^2-2m=4m^2+12m+9-2m=4m^2+10m+9\)
\(=4m^2+\dfrac{2.2m.10}{4}+\dfrac{100}{16}-\dfrac{100}{16}+9\)
\(=\left(2m+\dfrac{10}{4}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall m\)
Dấu ''='' xảy ra khi x = -5/4
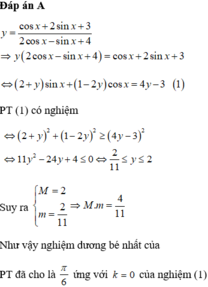


Đáp án C