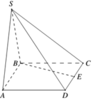
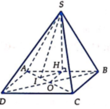
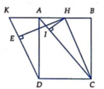
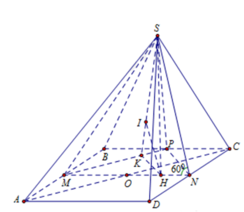
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a , BC= a tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD Tính theo a khoảng cách giữa hai đường thẳng BE và SC
A. a 30 10
B. a
C. a 3 2
D. a 5 5

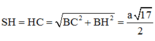
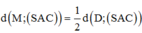
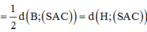
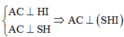
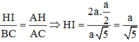
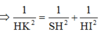
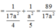
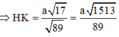
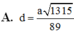
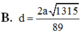
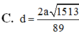
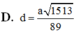


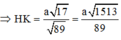

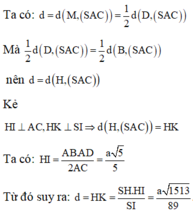
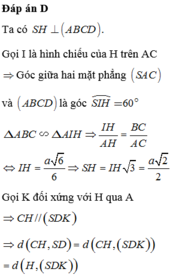

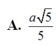
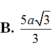
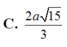
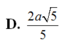
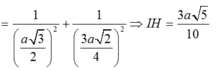




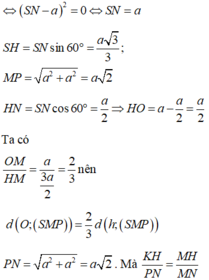
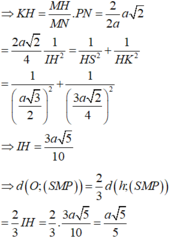

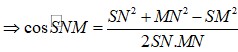
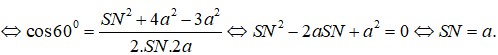

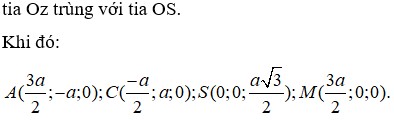
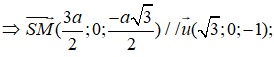
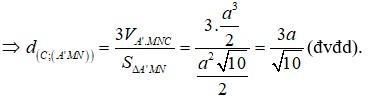
Chọn A
Chọn hệ trục tọa độ như hình vẽ, ta có H(0;0;0) , B(-a; 0; 0) và C(-a; a; 0), E(0; a; 0), S(0; 0; a 3 )
Ta có B E → = ( a ; a ; 0 ) , S C → = - a ; a ; - a 3 , E C → = ( - a ; 0 ; 0 )
Khi đó , B E → , S C → = ( - a 2 3 ; a 2 3 ; 2 a 2 )
Khoảng cách giữa BE và SC là