Một người cần làm một hình lăng trụ tam giác đều từ tấm nhựa phẳng để thể tích là 6 3 c m 3 . Để ít hao tốn vật liệu nhất thì người ta tính toán được độ dài cạnh đáy bằng a cm, cạnh bên bằng b cm Khi đó tích ab là:
A. 4 3
B. 2 6
C. 2 3
D. 6 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
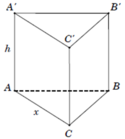
HD Giả sử hình lăng trụ tam giác đều cần làm là ABC.A'B'C' có độ dài AB = x,AA' = h
Khi đó S ∆ A B C = 3 4 x 2 và V A B C . A ' B ' C ' = S A B C . A A ' = 3 4 x 2 h
Theo giả thiết 3 4 x 2 h = 6 3 ⇒ h = 24 x 2
Để ít tốn vật liệu nhất thì diện tích toàn phần của khối lăng trụ ABC.A'B'C' là nhỏ nhất.
Gọi S t p là tổng diện tích các mặt của khối lăng trụ ABC.A'B'C' ,ta có
S t p = 2 S ∆ A B C + 3 S A B B ' A ' = 3 2 x 2 + 2 h x = 3 2 x 2 + 72 x
Khảo sát f ( x ) = 3 2 x 2 + 72 x trên ( 0 ; + ∞ ) ,ta được f (x) nhỏ nhất khi x = 2 3
Với x = 2 3 c m → h = 2 c m

Đáp án A
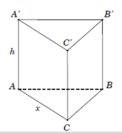
HD Giả sử hình lăng trụ tam giác đều cần làm là ABC.A'B'C' có độ dài AB = x, AA' = h
Khi đó 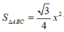 và
và ![]()
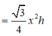
Theo giả thiết 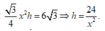
Để ít tốn vật liệu nhất thì diện tích toàn phần của khối lăng trụ ABC.A'B'C' là nhỏ nhất.
Gọi S t p là tổng diện tích các mặt của khối lăng trụ ABC.A'B'C',ta có
![]()
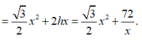
Khảo sát 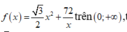 ta được f(x) nhỏ nhất khi x =
2
3
ta được f(x) nhỏ nhất khi x =
2
3
Với x = 2 3 => h = 2 cm

Đáp án B
Gọi R, h lần lượt là bán kính đáy và chiều cao của khối trụ
Chọ hệ trục tọa độ Oxy như hình vẽ với tứ giác ABCD là hình chữ nhật nối tiếp hình (E)

Gọi A x 0 ; y 0 x 0 > y 0 > 0 , khi đó ta có A B = 2 π R C D = h ⇔ 2 x 0 = 2 π R 2 y 0 = h ⇔ x 0 = π R y 0 = h 2
Thể tích khối trụ là V = π R 2 h = 2 x 0 2 π . y 0 mà A ∈ E ⇒ x 0 2 a 2 + y 0 2 b 2 = 1 ⇒ x 0 2 = a 2 b 2 b 2 − y 0 2

Đáp án C
Phương pháp:
Thể tích hình lăng trụ V = Sh
Diện tích toàn phần của lăng trụ: Stp = Sxq + 2.Sđáy
Cách giải:
Giả sử hình lăng trụ có đáy là tam giác đều cạnh a, có chiều cao h.


Dấu “=” xảy ra khi và chỉ khi
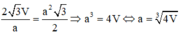
Đáp án A
(BĐT AM–GM)
Dấu bằng xảy ra: