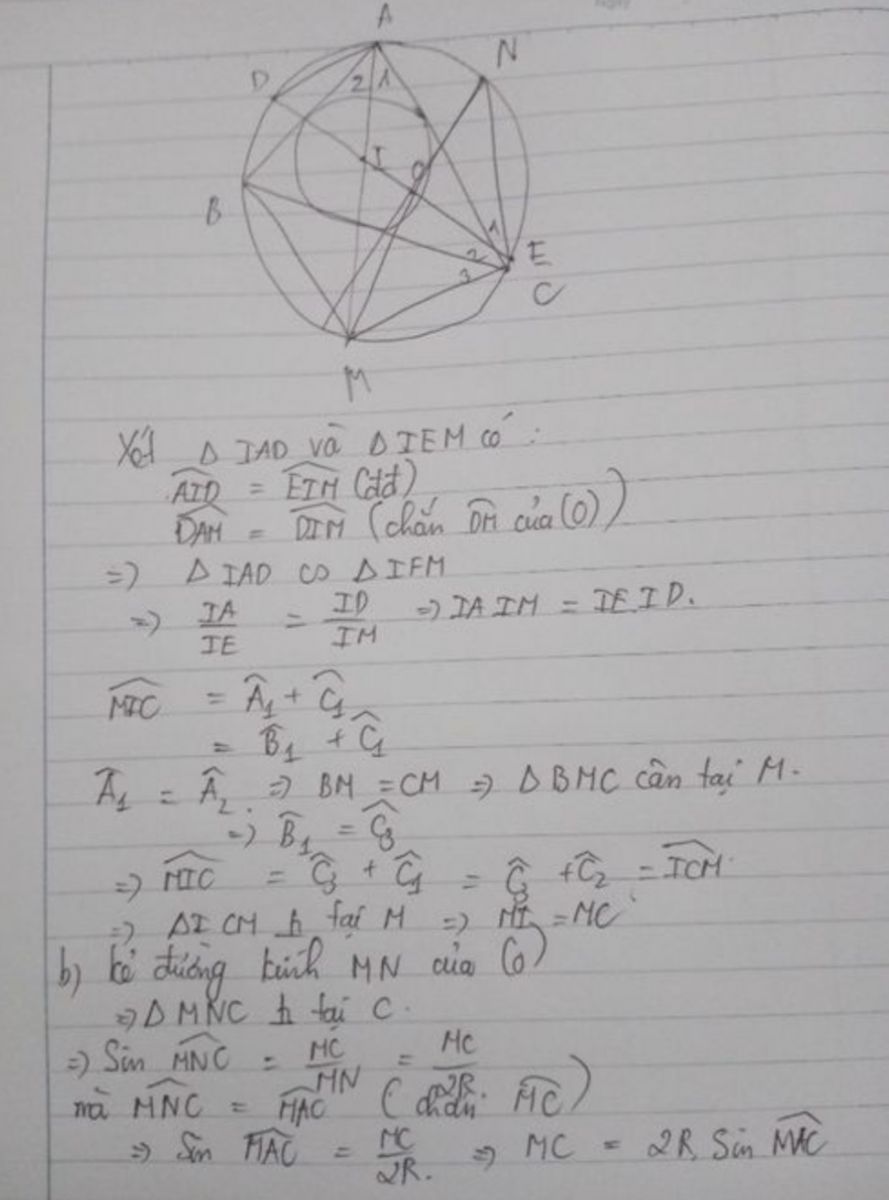Cho nữa đường tròn tâm O đường kính AB và điểm M bất kỳ thuộc nữa đường tròn( M khác A, B ) .Trên nữa mặt phẳng bờ AB chứa nữa đường tròn , vẽ tia tiếp tuyến Ax . Tia BM cắt AX tại I , tia phân giác của góc IBA cắt nữa đường tròn tại E , cắt AI tại H và cắt AM tại K , AE cắt BI tại F . Chứng minh : a/ Tam giác ABF cân . b/ BF2 = BM.BI c/ Tứ giác AKFH là hình thoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

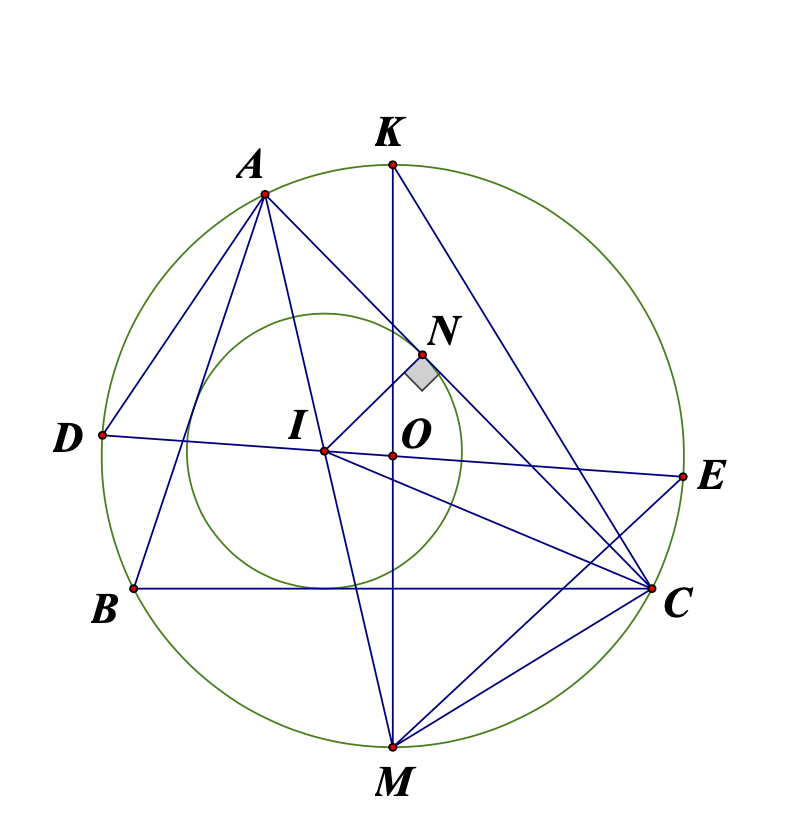
a) Vì ADME nội tiếp \(\Rightarrow\angle ADI=\angle IME\)
Xét \(\Delta IAD\) và \(\Delta IEM:\) Ta có: \(\left\{{}\begin{matrix}\angle AID=\angle EIM\\\angle ADI=\angle IME\end{matrix}\right.\)
\(\Rightarrow\Delta IAD\sim\Delta IEM\left(g-g\right)\Rightarrow\dfrac{IA}{IE}=\dfrac{ID}{IM}\Rightarrow IA.IM=ID.IE\)
ABMC nội tiếp \(\Rightarrow\angle MCB=\angle MAB=\dfrac{1}{2}\angle BAC\)
Ta có: \(\angle MCI=\angle MCB+\angle ICB=\dfrac{1}{2}\angle BAC+\dfrac{1}{2}\angle ACB\)
\(=\angle IAC+\angle ICA=\angle MIC\)
\(\Rightarrow\Delta MIC\) cân tại M \(\Rightarrow MI=MC\)
b) Kẻ \(OF\bot MC\Rightarrow F\) là trung điểm MC (\(\Delta OMC\) cân tại O)
\(\Rightarrow OF\) là phân giác \(\angle MOC\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOC=\dfrac{1}{2}.2\angle MAC=\angle MAC\)
\(\Rightarrow sinMOF=sinMAC\)
Ta có: \(MC=2MF=2.\dfrac{MF}{MO}.MO=2.sinMOF.R=2RsinMAC\)