Tung một con xúc sắc n lần. Tim giá trị nhỏ nhất của n để xác suất xuất hiện mặt 6 chấm hai lần nhỏ hơn 0,001
A. 60
B. 61
C. 62
D. 63
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 11 2019
Đáp án C
P = C n 2 1 6 2 5 6 n - 2 < 0 , 001
Thay các đáp án để xem n nhỏ nhất bằng bao nhiêu thỏa mãn hệ thức trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2020
a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)
CM
22 tháng 6 2018
Không gian mẫu: n Ω = 6 . 6 = 36
Gọi A là biến cố: ‘‘Tổng số chấm xuất hiện hai lần tung là một số nhỏ hơn 10’’.
⇒ A ¯ : ‘‘Tổng số chấm xuất hiện hai lần tung là một số không nhỏ hơn 10’’.
Tổng số chấm là một số không nhỏ hơn 10 nên số chấm xuất hiện là các cặp:
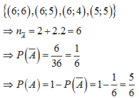
Chọn B.
TA
2 tháng 1 2023
Số phần tử của không gian mẫu là: `n(Ω)=6`
A: "Số chấm xuất hiện nhỏ hơn ba"
`-> n(A)= 2`
`=> P(A)=(n(Ω))/(n(A))=2/6=1/3`
`=>` A.
CM
29 tháng 5 2017
Gọi A i là biến cố “ mặt 4 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4.
Khi đó: A i là biến cố “ Mặt 4 chấm không xuất hiện lần thứ i”
Và P ( A i ¯ ) = 1 − P ( A i ) = 1 − 1 6 = 5 6
Ta có: A ¯ là biến cố: “ không có mặt 4 chấm xuất hiện trong 4 lần gieo”
Và A ¯ = A 1 ¯ . A 2 ¯ . A 3 ¯ . A 4 ¯ . Vì các A i ¯ độc lập với nhau nên ta có:
P ( A ¯ ) = P ( A 1 ¯ ) . P ( A 2 ¯ ) . P ( A 3 ¯ ) . P ( A 4 ¯ ) = 5 6 4
Vậy P ( A ) = 1 − P ( A ¯ ) = 1 − 5 6 4 .
Chọn đáp án A.
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 4 2023
1. Số phần tử của không giam mẫu: \(6.6=36\)
2. Biến cố A: có 6 phần tử (liệt kê 11, 22,...)
3. B: Ứng với mỗi lần tung thứ nhất, lần tung thứ 2 luôn có 2 biến cố thuận lợi để tổng 2 lần tung chia hết cho 3 (ví dụ lần 1 bằng 1 thì lần 2 bằng 2 hoặc 5). Do đó có tổng cộng \(6.2=12\) biến cố thuận lợi
4. C: Số biến cố thuận lợi là: \(5+4+3+2+1=15\) (ứng với lần tung thứ nhất lần lượt bằng 6, 5, 4, 3, 2)
Đáp án C