Gọi x, y là các số thực dương thỏa mãn log 9 x = log 12 y = log 16 x + y và x y = − a + b 2 , với a, b là hai số nguyên dương. Tính P = a . b
A. P=6
B. P =5
C.P=8
D. P = 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu một trong các số \(x+y-z;y+z-x;z+x-y\) bằng 0 thì cả 3 số đều bằng 0 và dẫn đến \(x=y=z=0\), mâu thuẫn
Từ giả thiết ta có : \(\begin{cases}x\log y\left(y+z-x\right)=y\log x\left(z+x-y\right)\\y\log z\left(z+x-y\right)=z\log y\left(x+y-z\right)\\z\log x\left(x+y-z\right)=x\log z\left(y+z-x\right)\end{cases}\)
Xét đẳng thức thứ nhất ta có :
\(x\log y\left(y+z-x\right)=y\log x\left(z+x-y\right)\Leftrightarrow x\log y=y\log x.\frac{z+x-y}{y+z-x}\) \(\Leftrightarrow x\log y+y\log x=y\log x\left(\frac{z+x-y}{y+z-x}+1\right)\Leftrightarrow x\log y+z\log x=y\log x\frac{2z}{y+z-x}\)
Biến đổi tương tự với đẳng thức thứ hai ta có :
\(y\log z+z\log y=z\log y\frac{2z}{z+z-y}\)
Ta thấy rằng : \(x^y.y^x=y^z.z^y\Leftrightarrow x\log y+y\log x=y\log z+z\log y\)
Do đó ta cần có :
\(y\log x\frac{2z}{y+z-x}=z\log y\frac{2z}{z+x-y}\Leftrightarrow y\log x\left(z+x-y\right)=x\log y\left(y+z-x\right)\), đúng
Do đó ta được : \(x^yy^x=y^z.z^y\)
Chứng minh tương tự ta có : \(y^zz^y=z^x.x^z\)
=> Điều phải chứng minh

Đáp án D
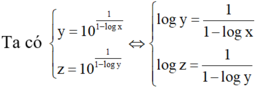
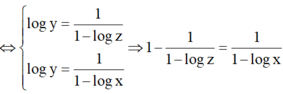
⇔ log z - 1 log z = 1 1 - log x
⇔ 1 - log x = log z log z - 1
⇔ log x = - 1 log z - 1 ⇔ x = 10 1 1 - log z .
Đáp án B
Đặt log 9 x = log 12 y = log 16 x + y = t ⇔ x = 9 t y = 12 t và x + y = 16 t
Suy ra 9 t + 12 t = 16 t ⇔ 3 t 2 + 3 t .4 t − 4 t 2 = 0 ⇔ 3 4 t 2 + 3 4 t − 1 = 0 ⇔ 3 4 t = − 1 + 5 2
Vậy x y = 9 t 12 t = 3 4 t = − 1 + 5 2 = − a + b 2 ⇔ a = 1 b = 5 ⇒ P = a b = 5