Hàm số y = sin x Đồng biến trên mỗi khoảng:
A. - 3 π 2 + k 2 π ; 5 π 2 + k 2 π với k ∈ R
B. π 2 + k 2 π ; π + k 2 π với k ∈ R
C. π 2 + k 2 π , 3 π 2 + k 2 π với k ∈ R
D. - π 2 + k 2 π , π + k 2 π với k ∈ R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)

Tập xác định: D = R; y′ = x 2 − (1 + 2cosa)x + 2cosa
y′= 0 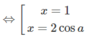
Vì y’ < 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì 2cosa ≤ 1
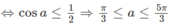
(vì a ∈ (0; 2 π ).

Đáp án D
Đặt t = cos x ⇒ t ∈ − 1 ; 1 ⇒ y = f t = 2 t + 1 t − m
Ta có f ' t = 2 m + 1 t − m 2 sin x
Hàm số đồng biến trên khoảng:
0 ; π ⇒ f ' t > 0 t − m ≠ 0 ⇔ 2 m + 1 sinx > 0 m ≠ t ⇔ m > − 1 2 m ≥ 1 m ≤ − 1 ⇒ m ≥ 1

Đáp án D
Đặt t = c osx ⇒ t'=-sinx < 0 ; ∀ x ∈ 0 ; π suy ra t ∈ − 1 ; 1 .
Khi đó
y = f t = 2 t + 1 t − m ⇒ f ' t = − 2 m + 1 t − m 2 x t ' .
Hàm số đã cho đồng biến trên khoảng 0 ; π
⇔ f ' t > 0 ; ∀ t ∈ − 1 ; 1 ⇔ − 2 m + 1 t − m 2 x t ' > 0 ; ∀ t ∈ − 1 ; 1
mà t ' < 0 suy ra
2 m + 1 t − m 2 > 0 ; ∀ t ∈ − 1 ; 1 .
⇔ 2 m + 1 > 0 t = m ∉ − 1 ; 1 ⇔ m > − 1 2 m ∉ − 1 ; 1 ⇔ m > − 1 2 1 2 ≥ 1 m ≤ − 1 ⇔ m ≥ 1 là giá trị cần tìm

Đáp án B
Đặt ![]() .
.
Với 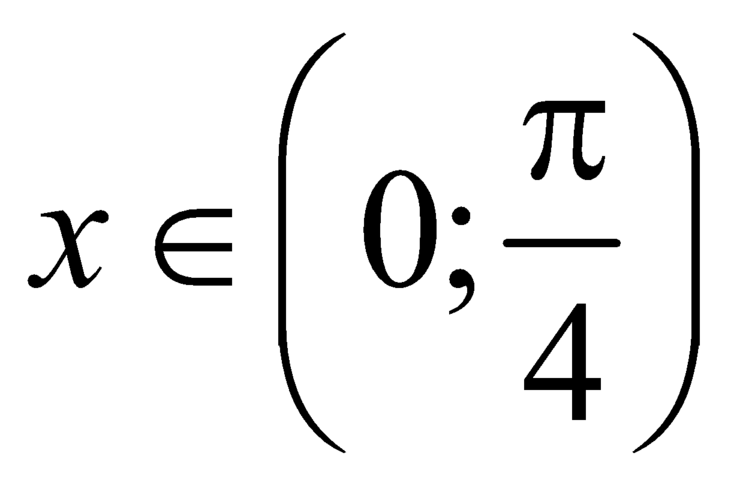 thì
thì ![]() , hàm số trở thành
, hàm số trở thành ![]() .
.
Đạo hàm 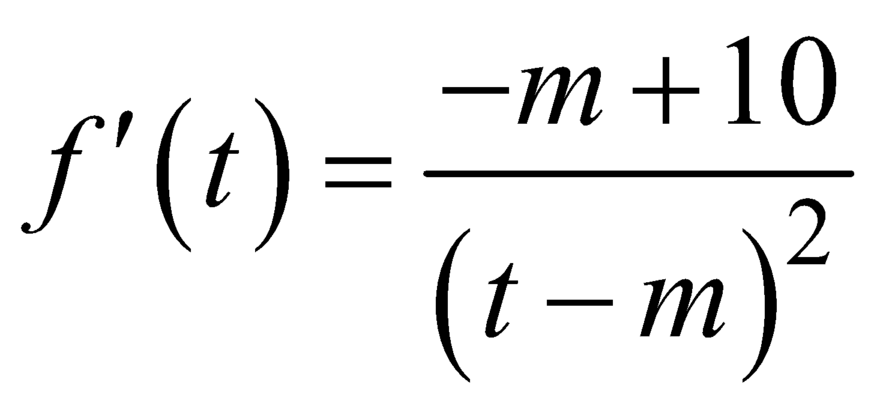 .
.
Hàm số đồng biến trên ![]() khi
khi
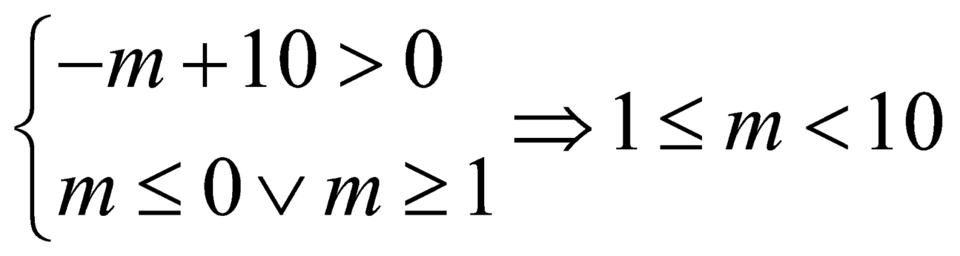 .
.
Vậy có 9 giá trị nguyên của m
Đáp án D